Unsurpervised Learning
Unsupervised Learning
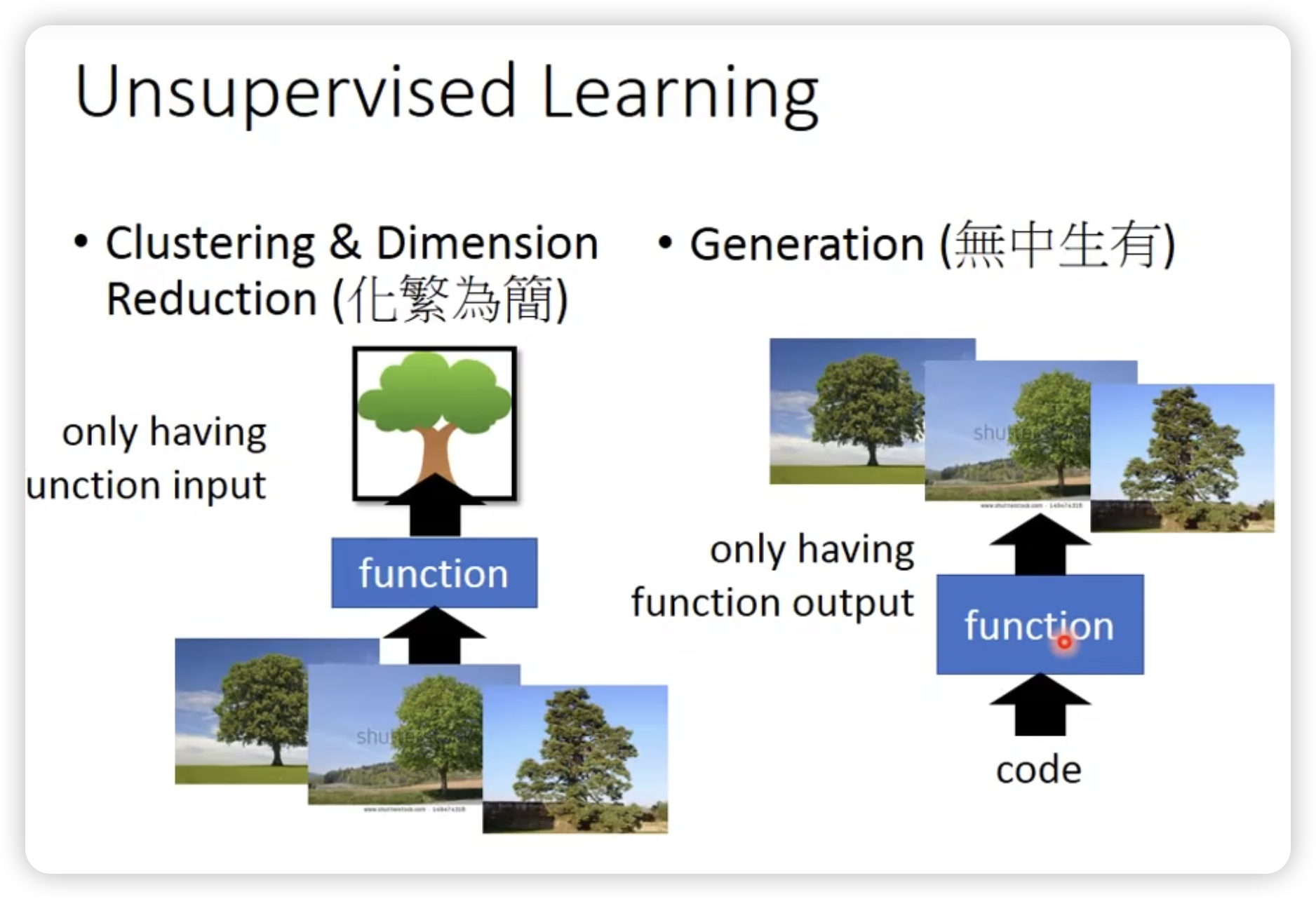
分为两类,降维和生成。

-
K-mean
一开始从training data里sample出k个点init,然后不断迭代,更新每个点的位置,使得每个点周围的点尽可能的接近它。 -
Hierarchical Agglomerative Clustering
每次合并距离最近的两个点,直到只剩下一个点。
这棵树上,比较早分支就比较不像(比如root)
然后可以切一刀,划分出不同的cluster类。(可以比较好决定cluster的数量)
但是cluster太过绝对!
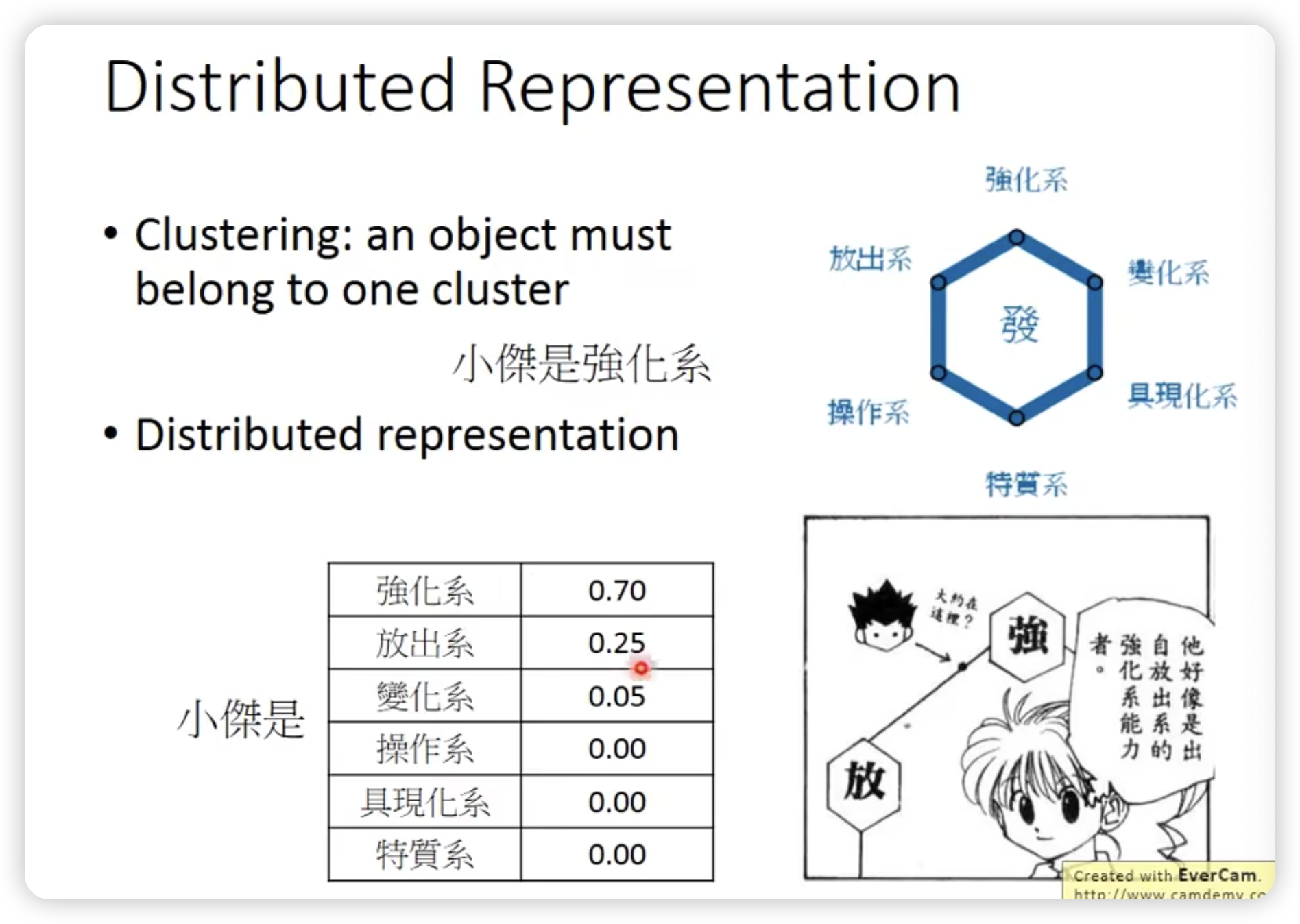
Distributed representation <—> Dimension reduction
其实是一样的事情
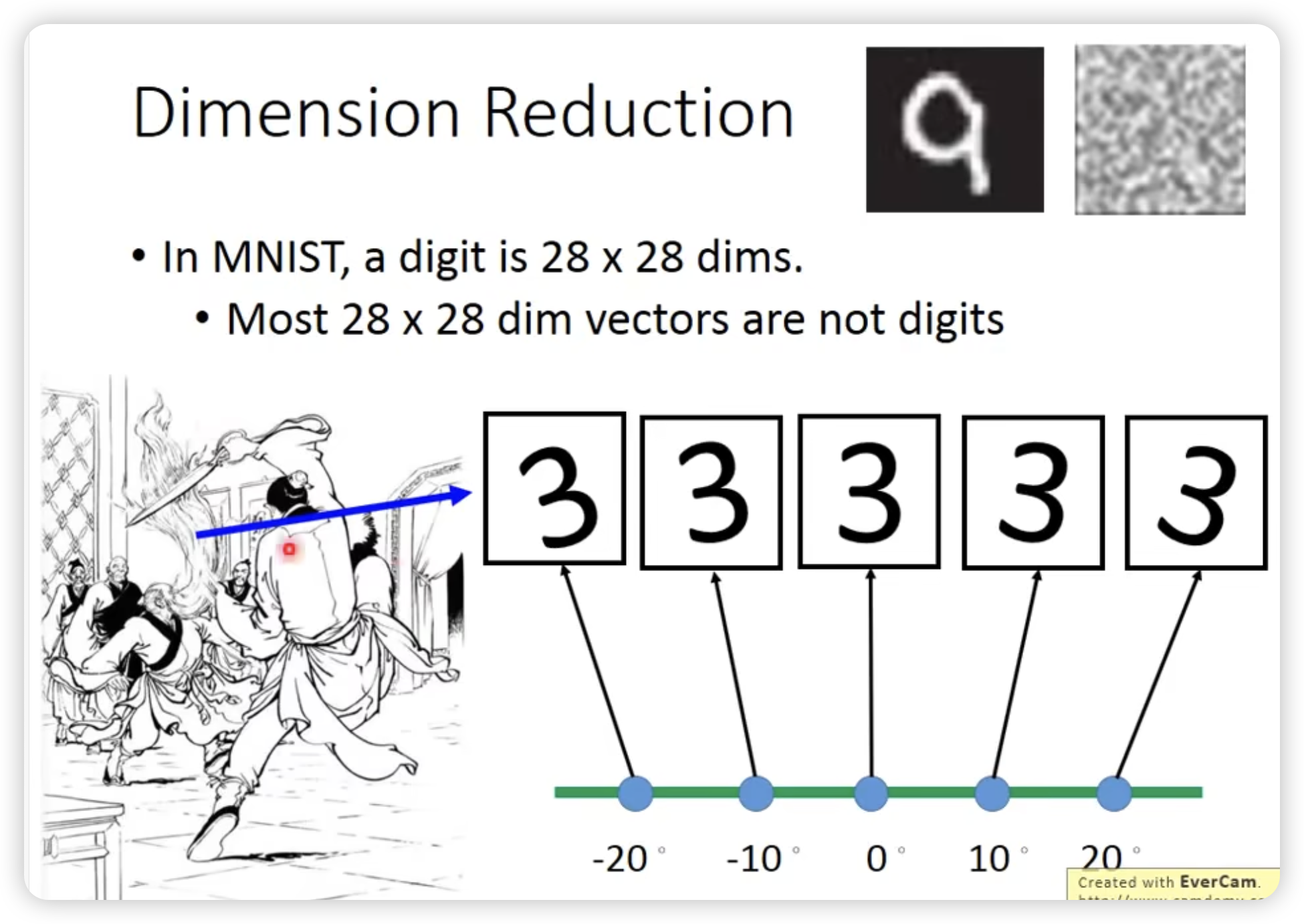
Demension Reduction
- 去掉无用feature(很多时候不好用)
- PCA(Principal Component Analysis)
PCA
z = Wx
目的:找这个W
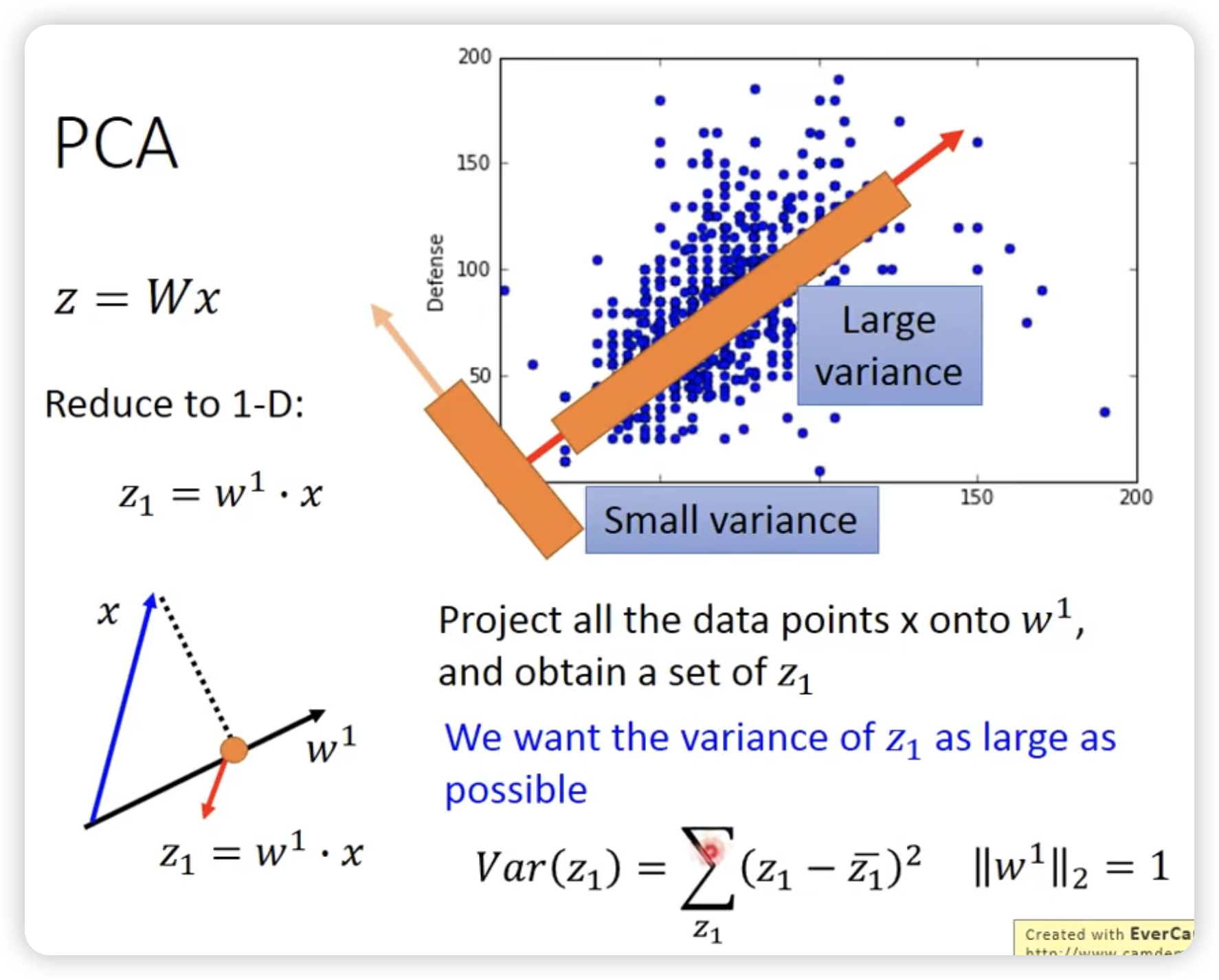

需要project到几维是自己决定的
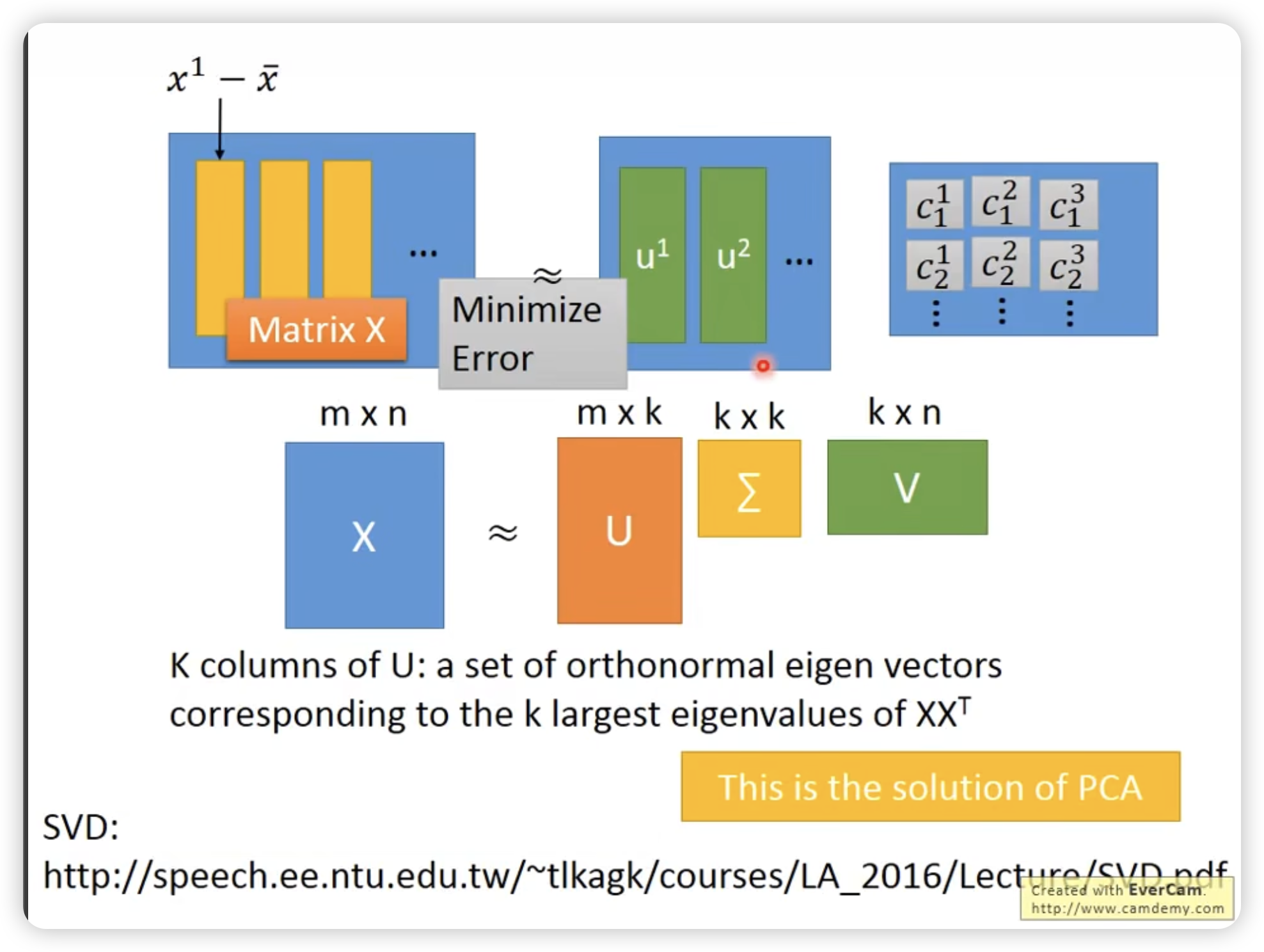
如何解PCA ?



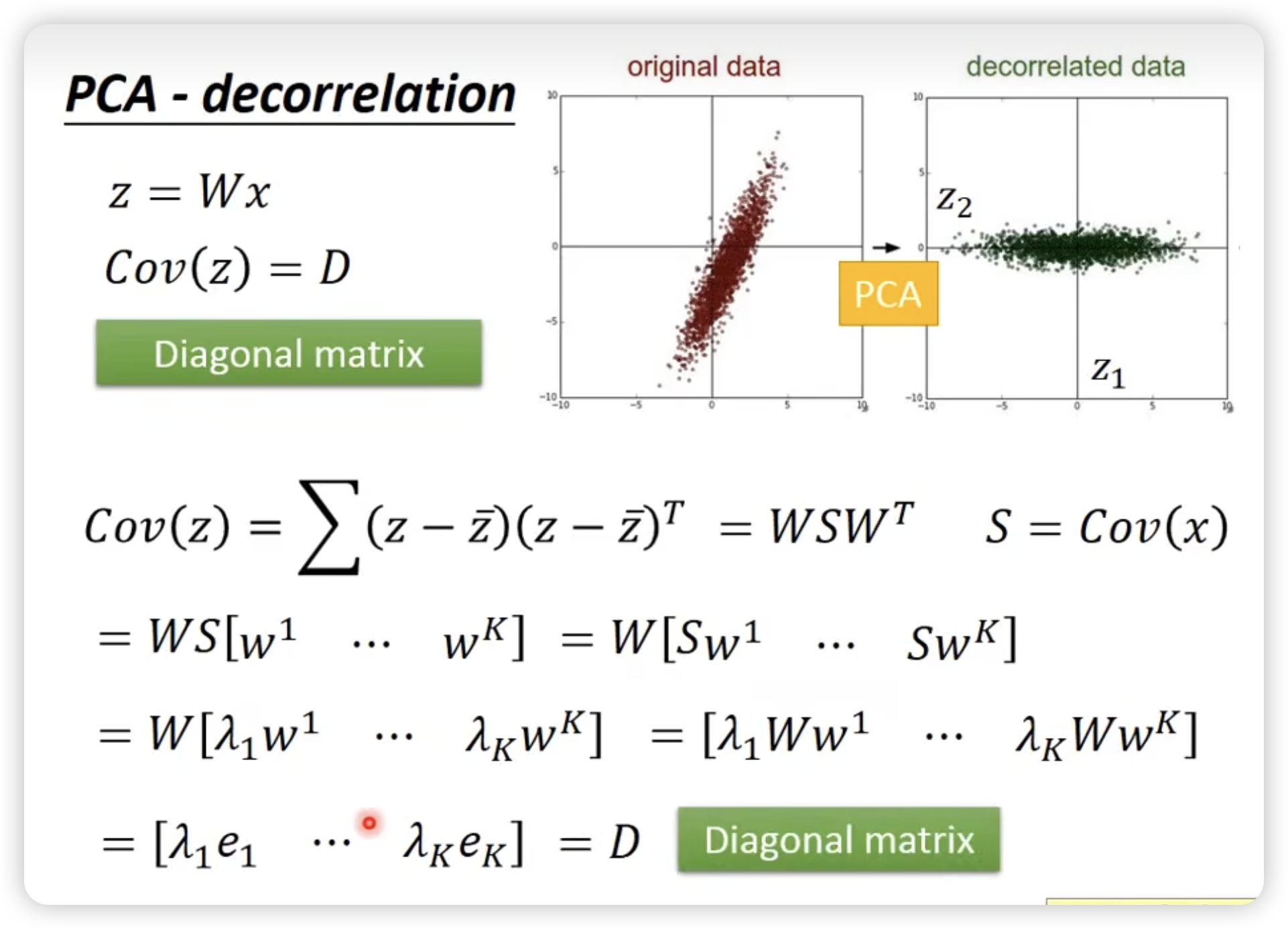
新的z的feature的Cov是diagnal的!!!
很多比较简单的model需要这个要求(不同feature之间没有corelation),避免overfitting
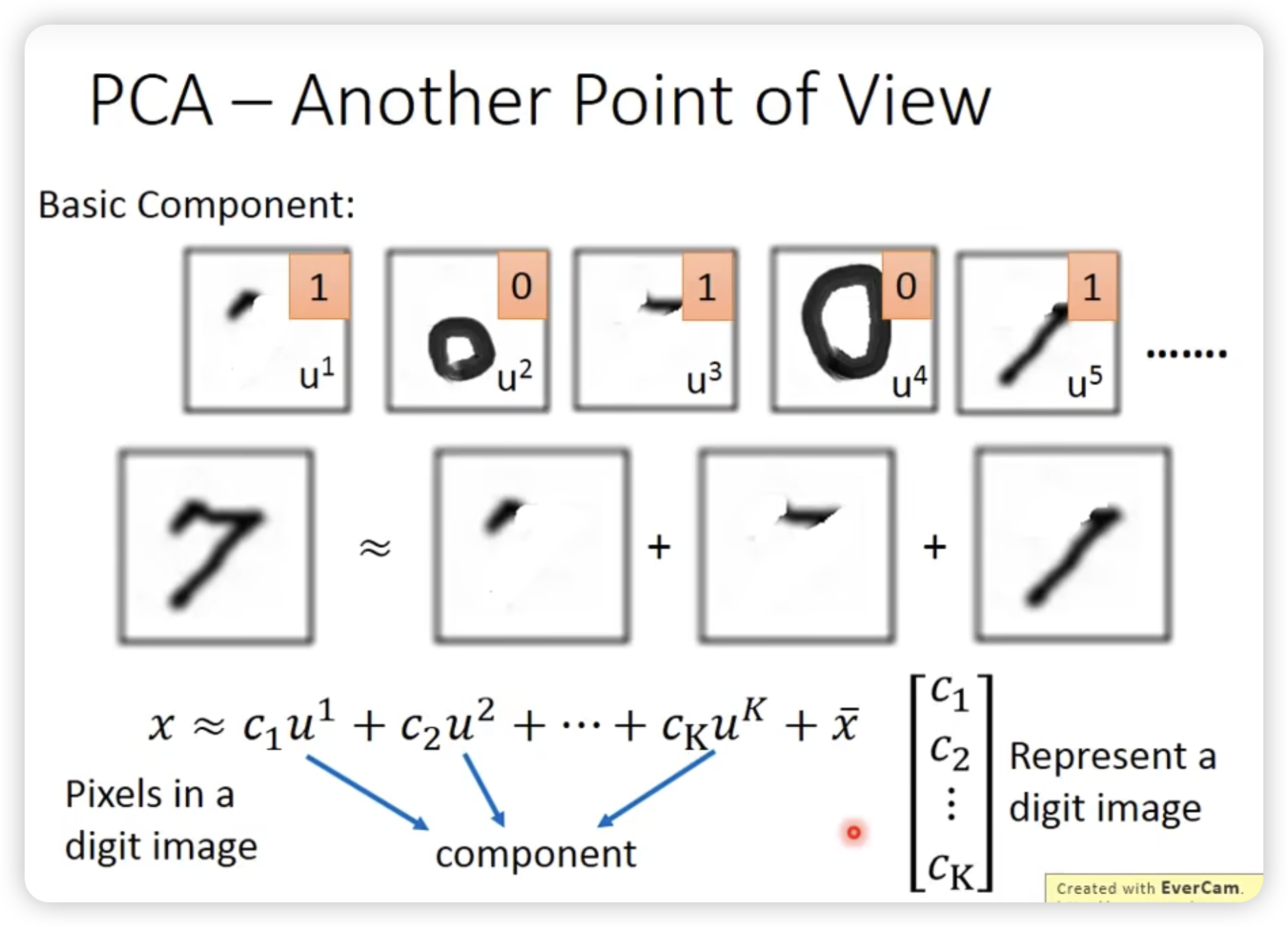
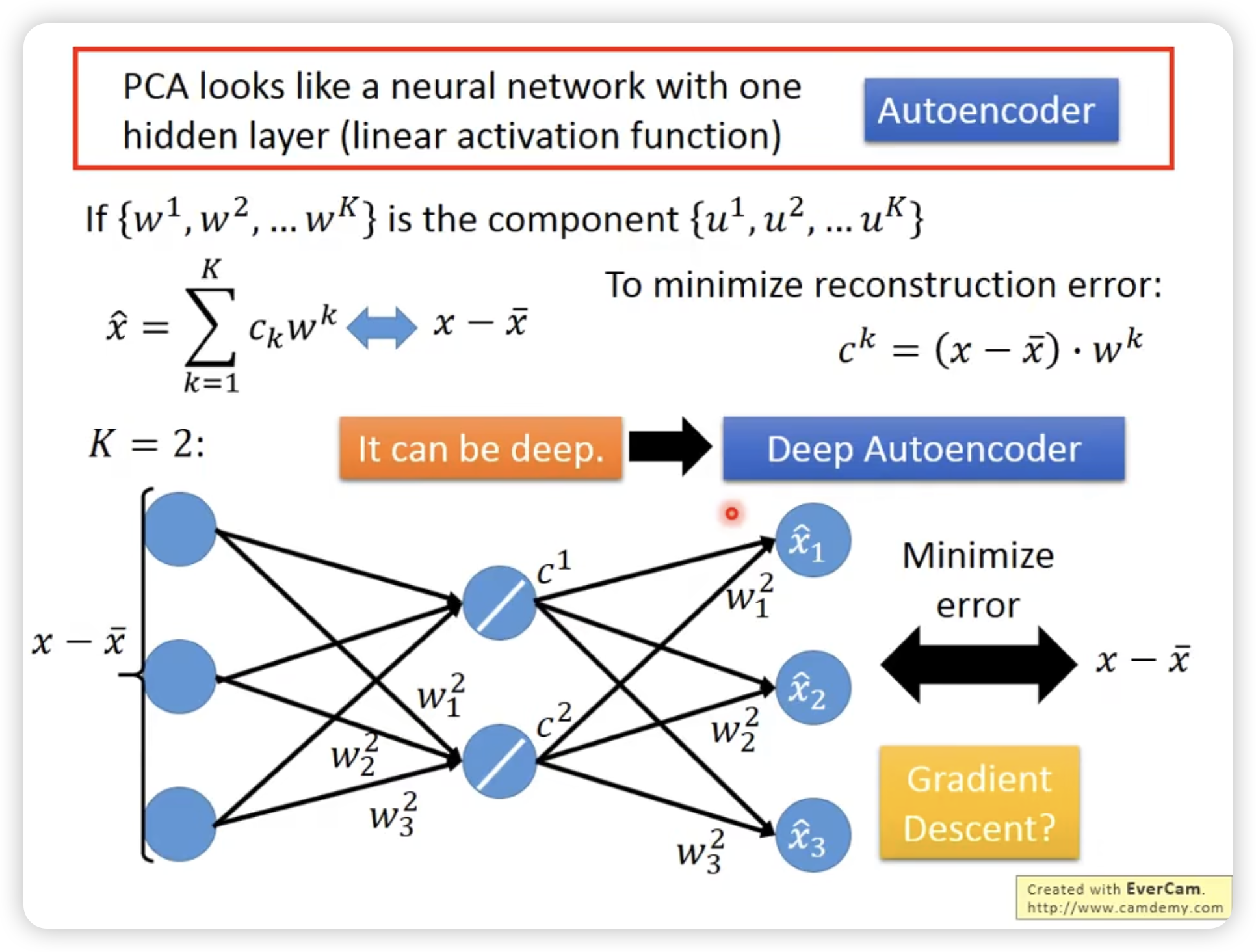
另外一个理解PCA的视角

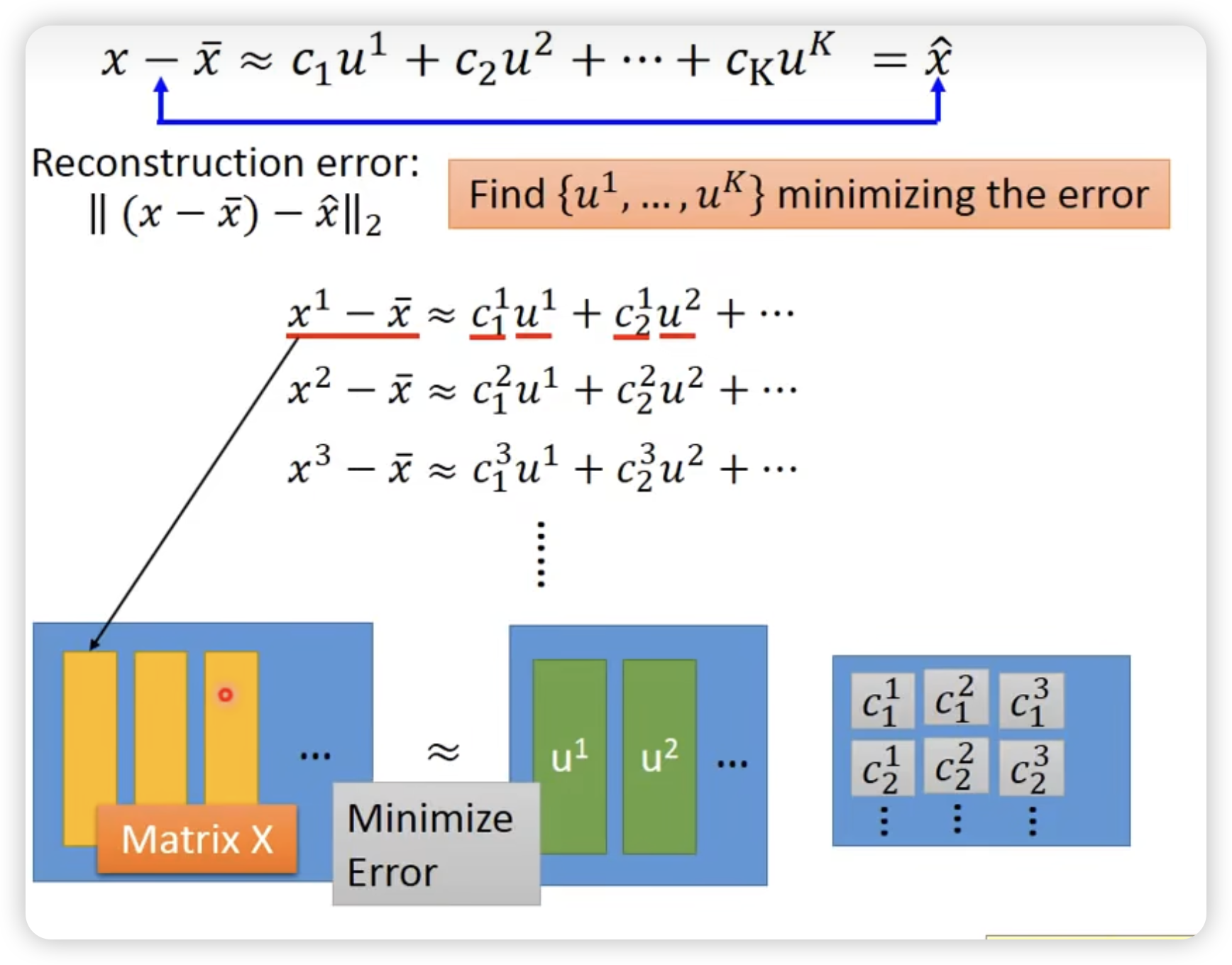

甚至可以表示为一个一层的neural network


PCA可以做加法,也可以减法。意味着很大情况下不是各个component的相加。(比如多画一些,再剪掉一些其它的component)
不让做减法的话,就是LDA(Linear Discriminant Analysis)

保证所有值都是正的,只让做加法的组合。
这里的正负指的是component的系数,而不是component本身的正负。
Matrix factorization
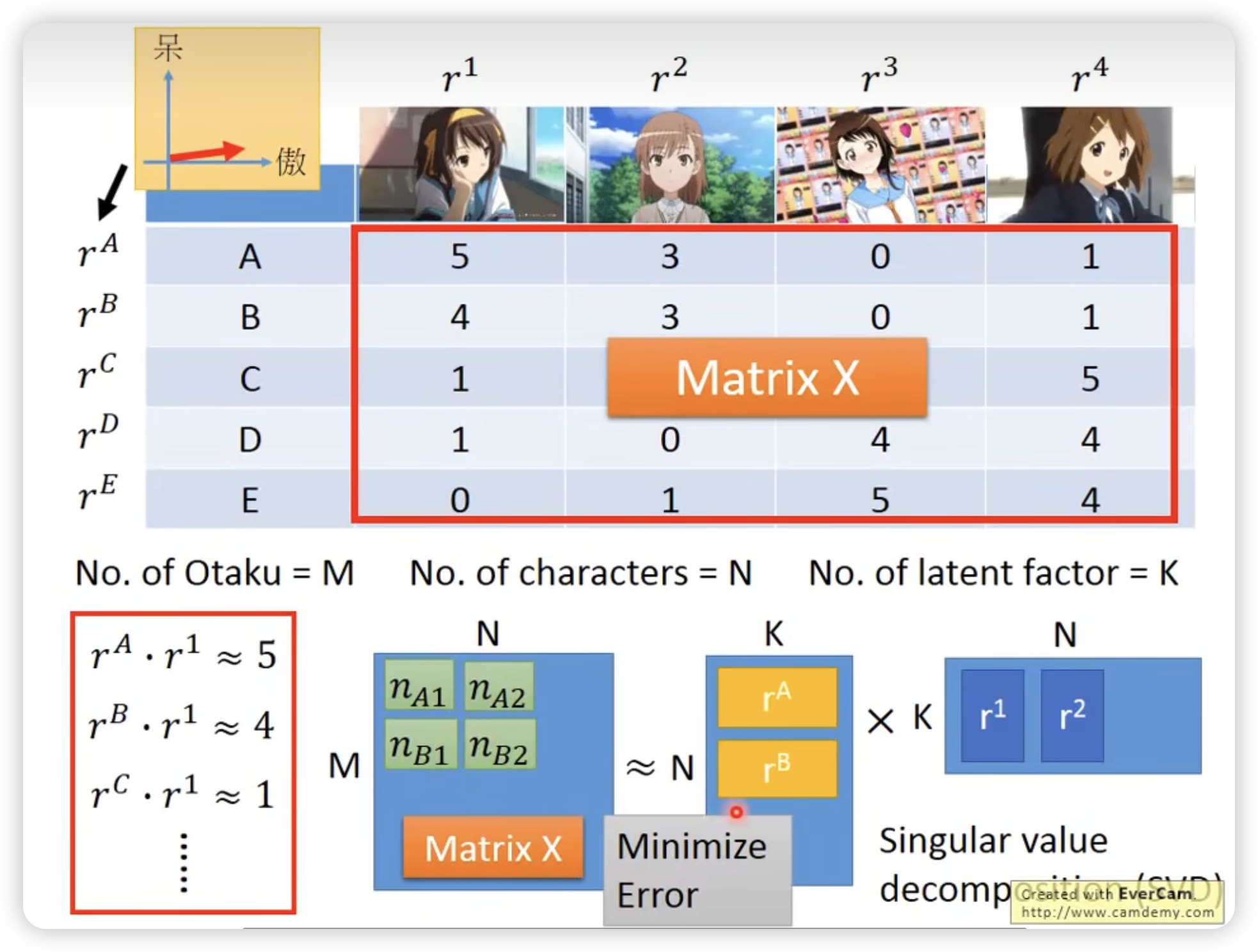
对于有missing data的情况,可以用gradient descent设计loss时不考虑来规避。

结果:
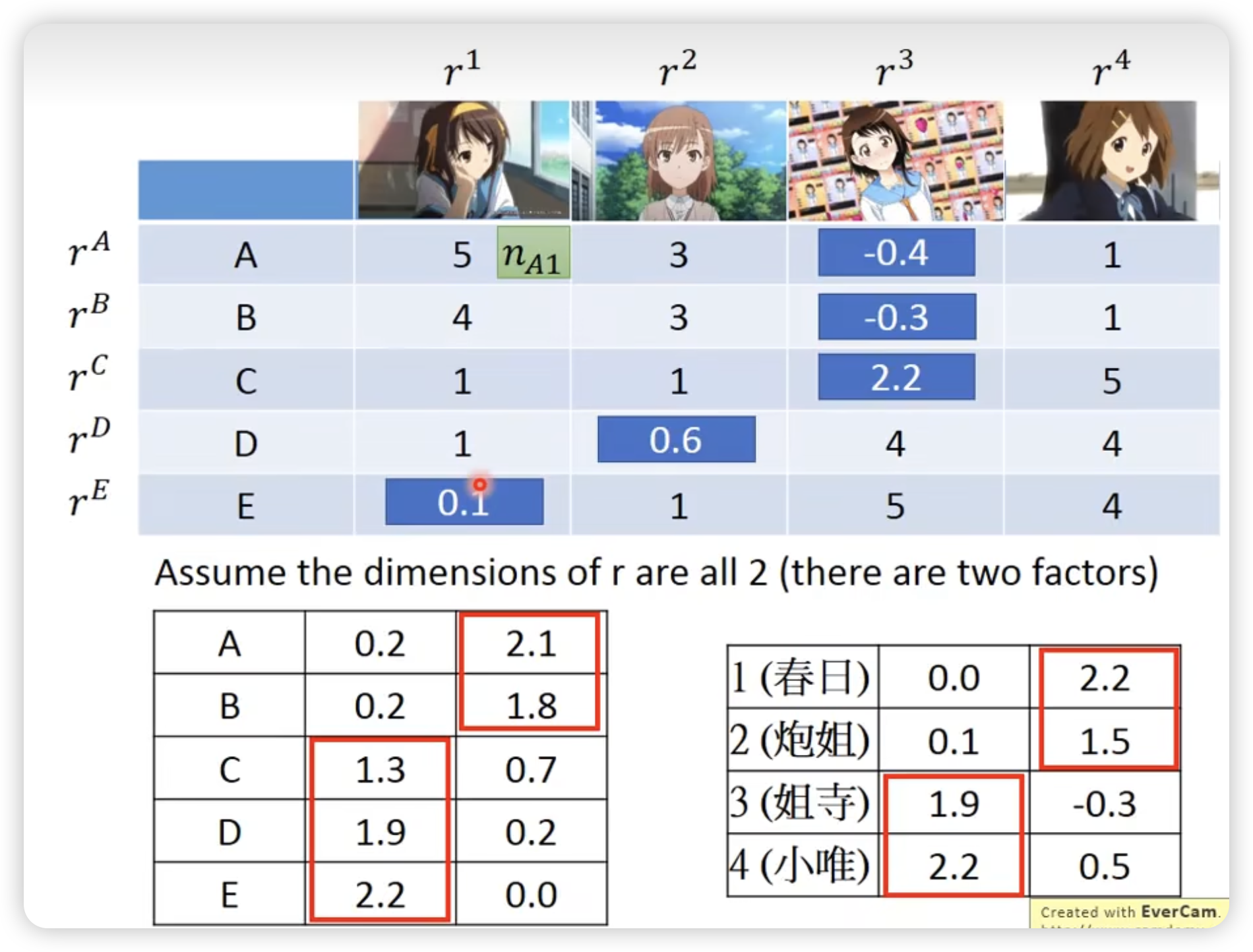
甚至可以反过来填充未知单元格,这个思路可用在推荐系统中。

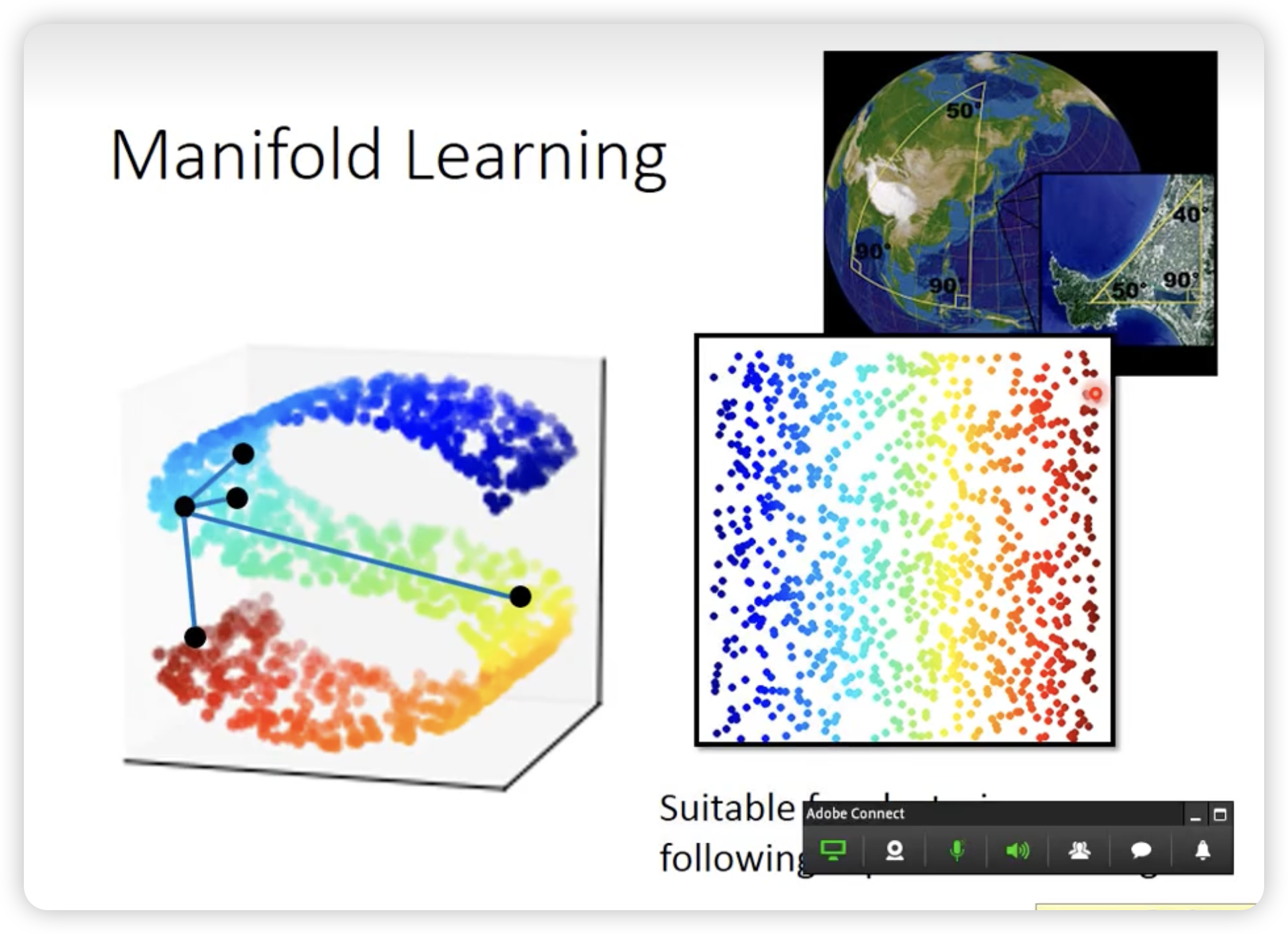
Manifold Learning
LLE(Locally Linear Embedding)
一般在曲面上,欧式距离近的点对不一定是相似的。
我们使用manifold learning来摊平这个曲面,去做更准确的降维。
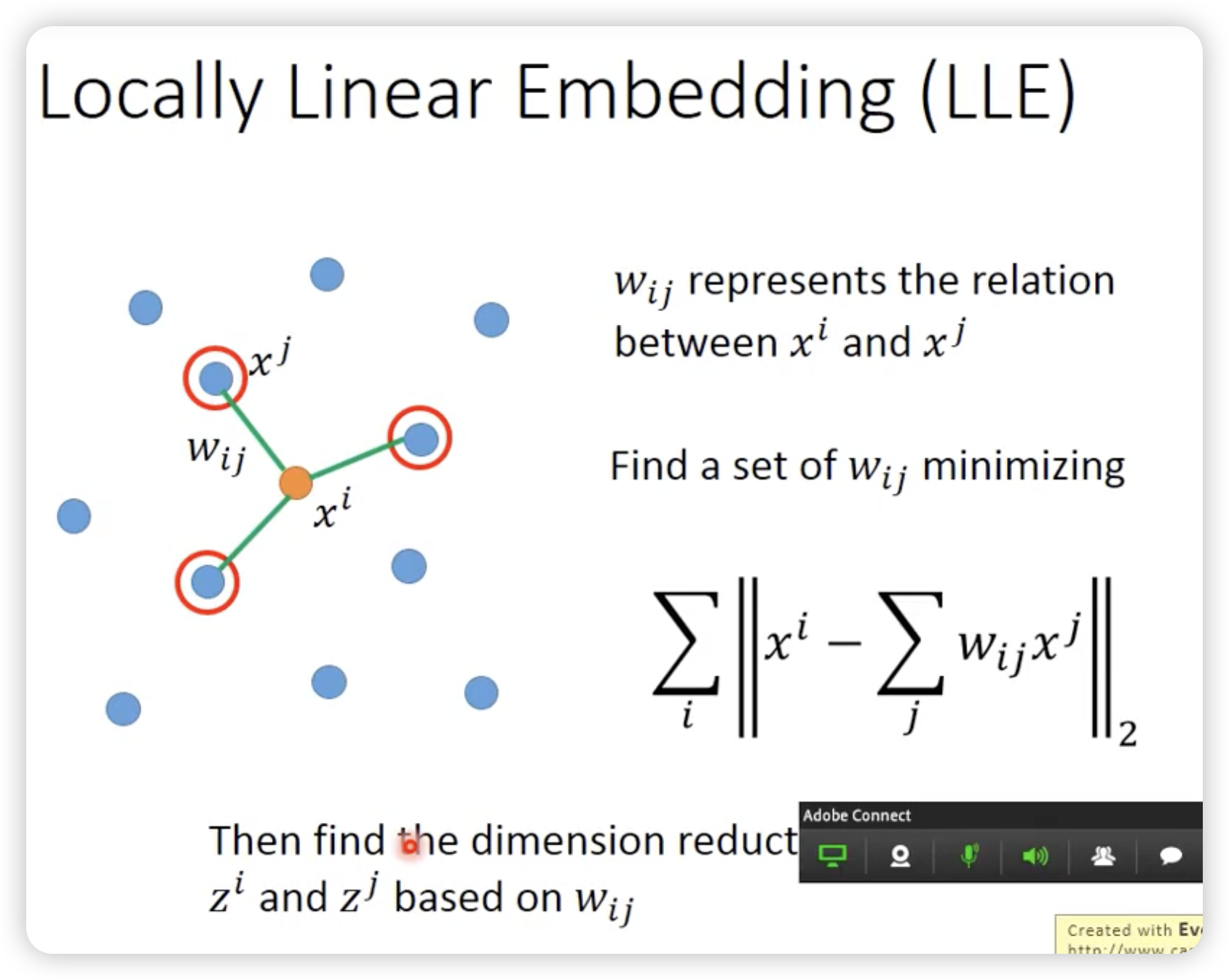

找一组wij,确定原始空间的邻居关系,使得在新的降维空间中的邻居关系尽可能的保持。
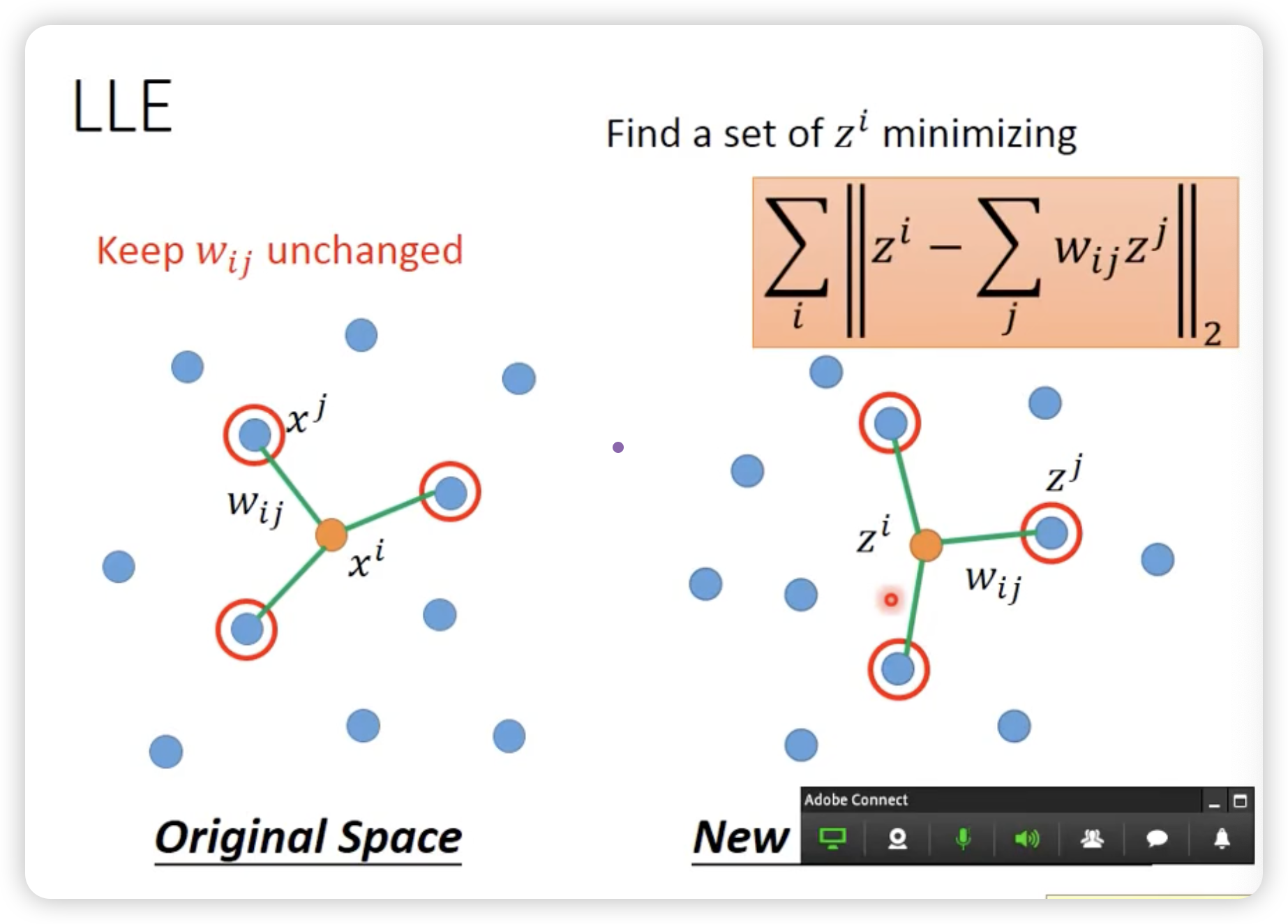
LLE并没有一个明确的function去做降维,Z就是完全凭空找出来的,这样一个好处就是只知道x的关系,就可以找到z。
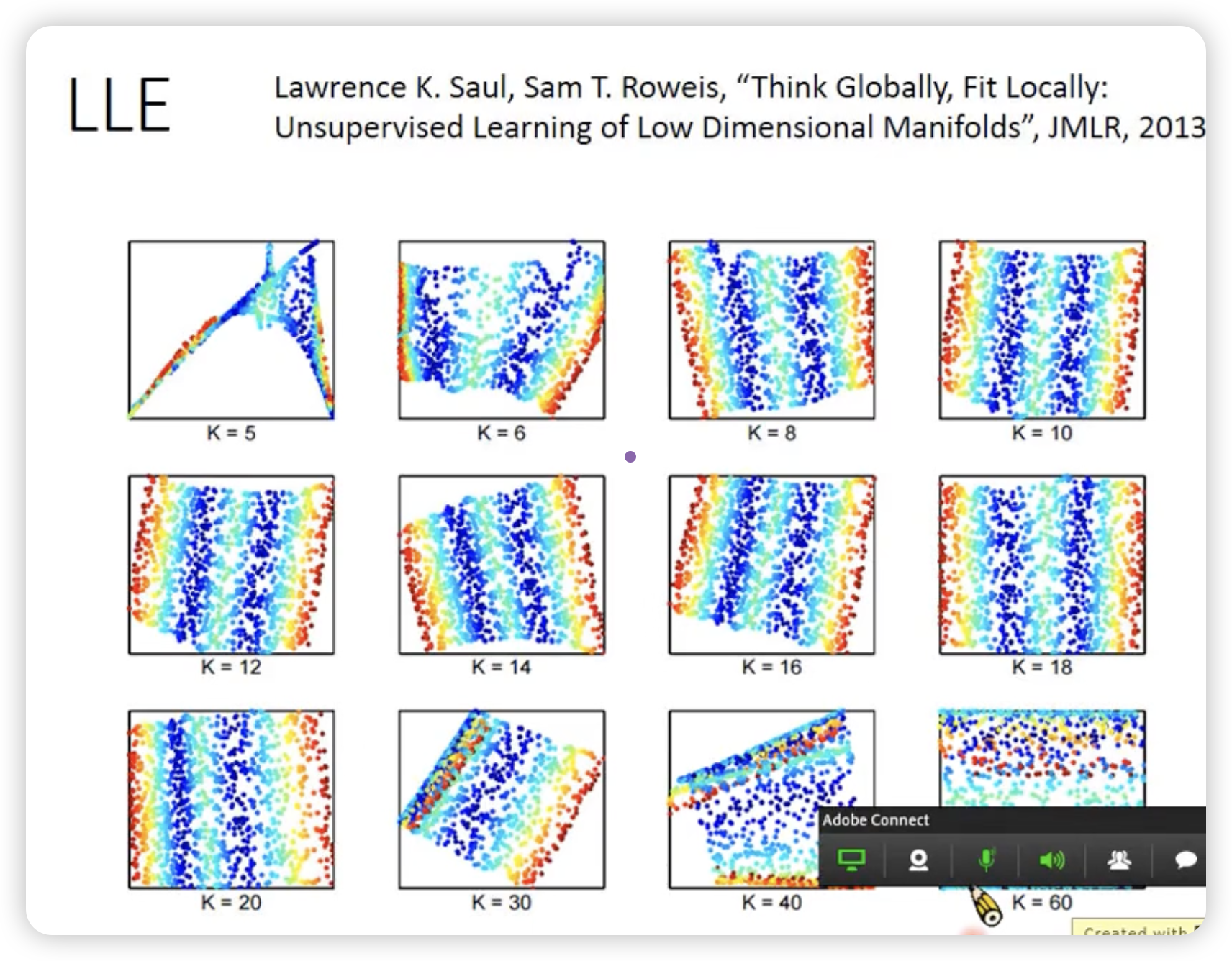
例子:
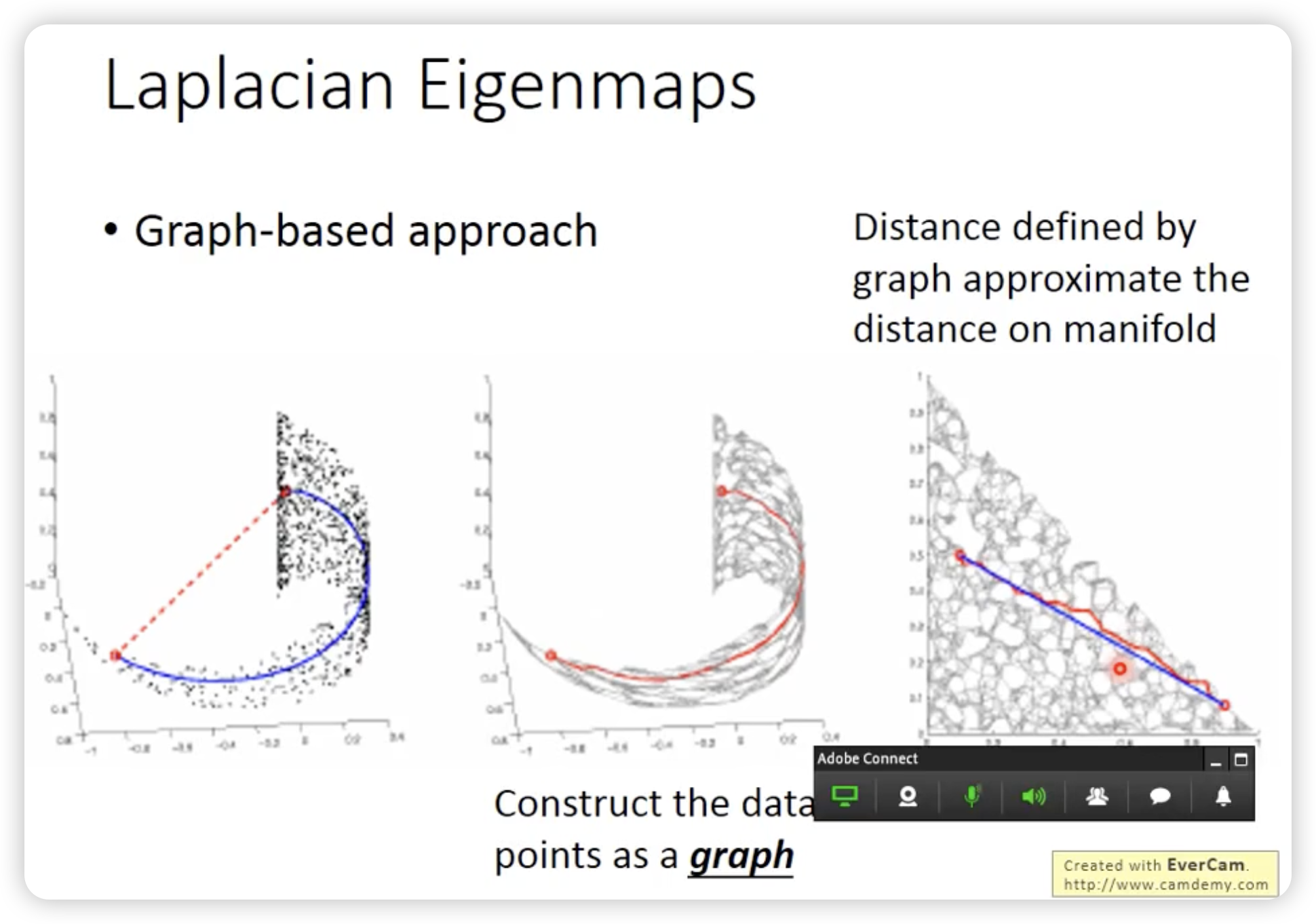
Laplacian Eigenmaps
不能简单看欧式距离,要看high density的距离,这个距离近才是真的接近。

这张图中的数学公式用于定义一个优化目标函数:
• 是有监督学习的部分,用于拟合已知标签。
• 是无监督的正则化部分,通过最小化 确保标签预测在图结构上是平滑的。
同样的道理用在unsupervised learning上,就是Laplacian Eigenmaps。

但是前面的东西有个问题,只是假设相近的点在降维后也是相近的,但是没有考虑到相远的点在降维后也是相远的。
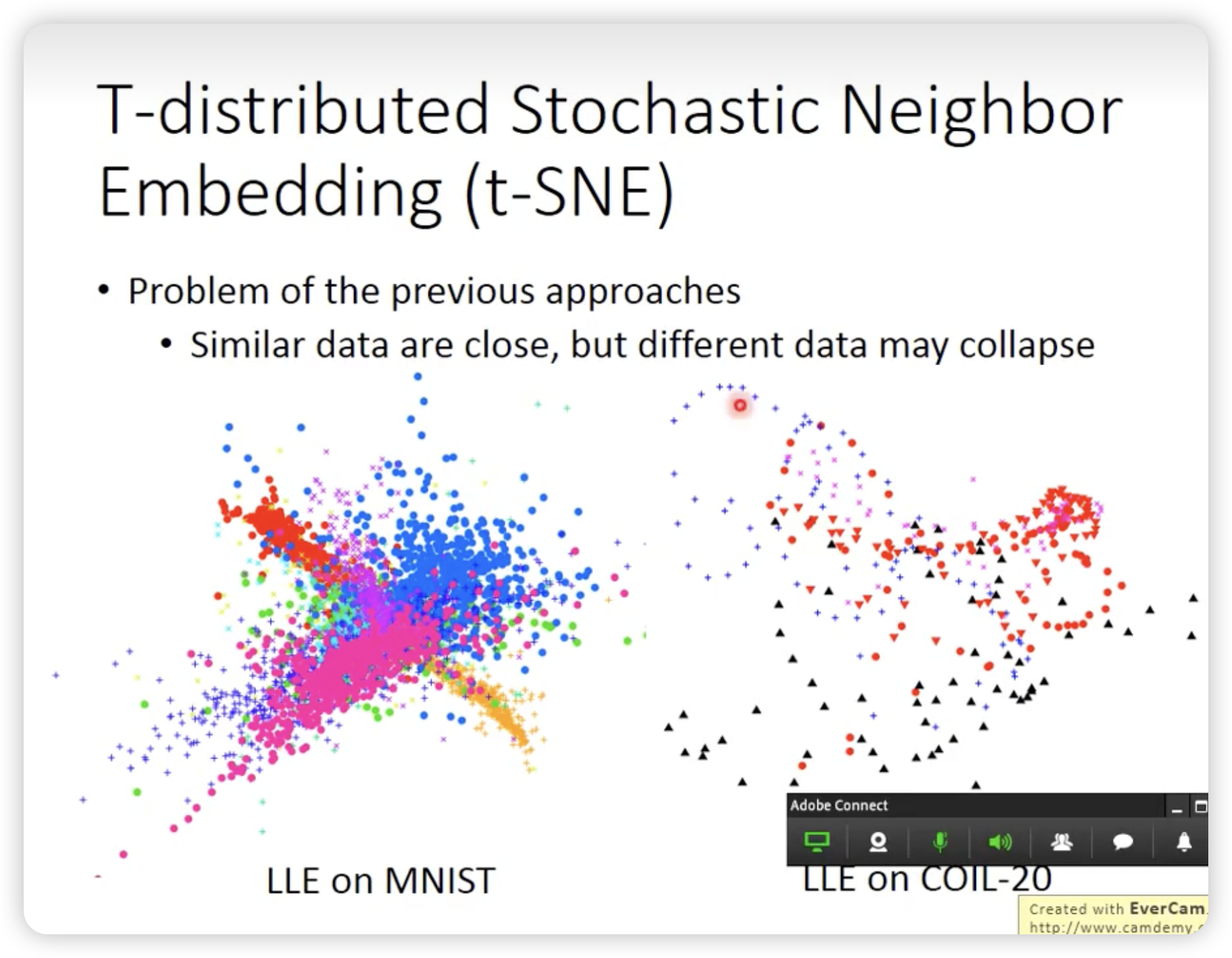
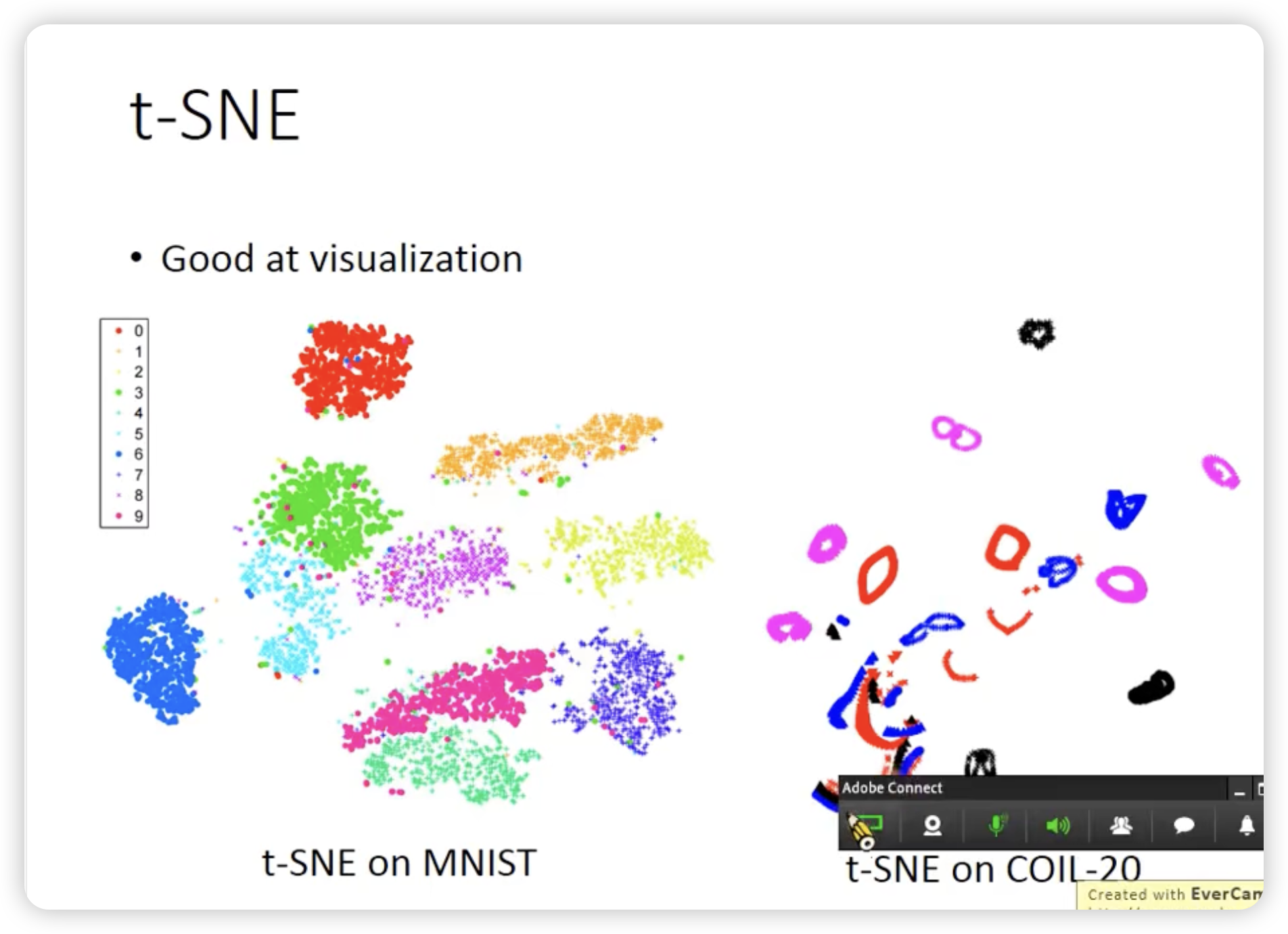
所以我们需要一个新的方法,t-SNE

t-SNE没有办法做到dynamic的添加x,所以很多情况下,t-SNE只是用来可视化数据。
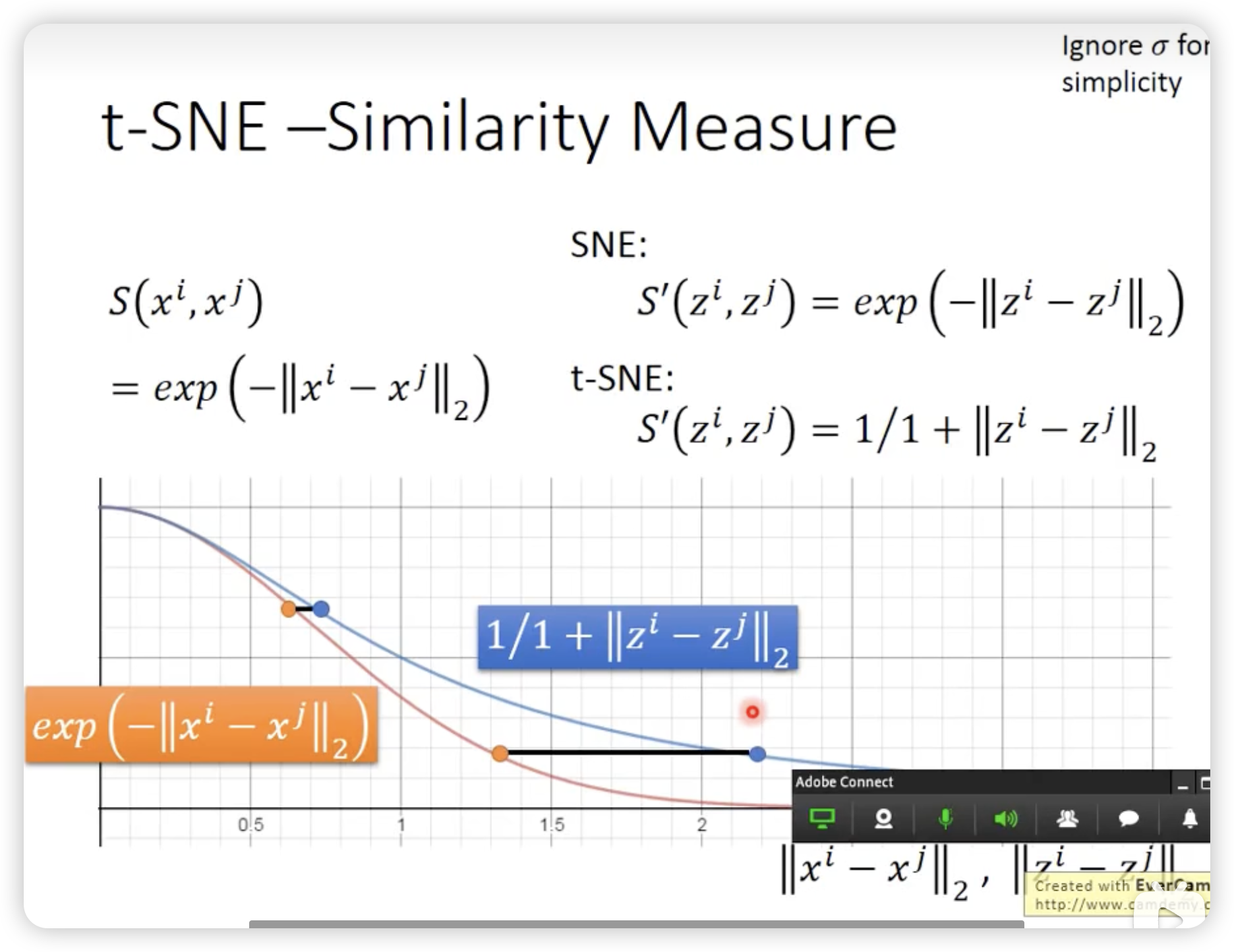
t-SNE的分布是heavy-tailed的,所以对于原来差距大的点,降维后的差距会更大。