DRL: Actor-Critic Method

detect0530@gmail.com

基本概念

Discounted Return $U_t$

这个东西是一个随机变量，随机性由两部分构成，第一是Policy function给定状态s后选择的action。第二是State transition function给定状态s和action a后转移到下一个状态s’的概率。

Action-value Function Q(s,a)

给定状态s和action a，这个函数返回的是在这个状态下采取这个action的期望回报。注意这个回报和策略函数$\pi$有关，因为策略函数决定了在这个状态下采取哪个action。

Optimal Action-value Function $Q^*(s,a)$

选择一个在当前状态和动作下最优的策略函数$\pi$,让期望回报最大。

State-value Function $V_{\pi}(s)$

$V_{\pi}(s_t)$是对一个状态的评价，这个评价是基于决策函数$\pi$的，给定状态s，则可以用来评价决策函数$\pi$的好坏。

Deep Q-network (DQN)

Approximate the Q Funtion

我们只需要知道$Q^*(s,a)$的函数表达，就可以知道在s下走哪一个action最优，于是我们寄希望于用nenural network来近似拟合这个函数。

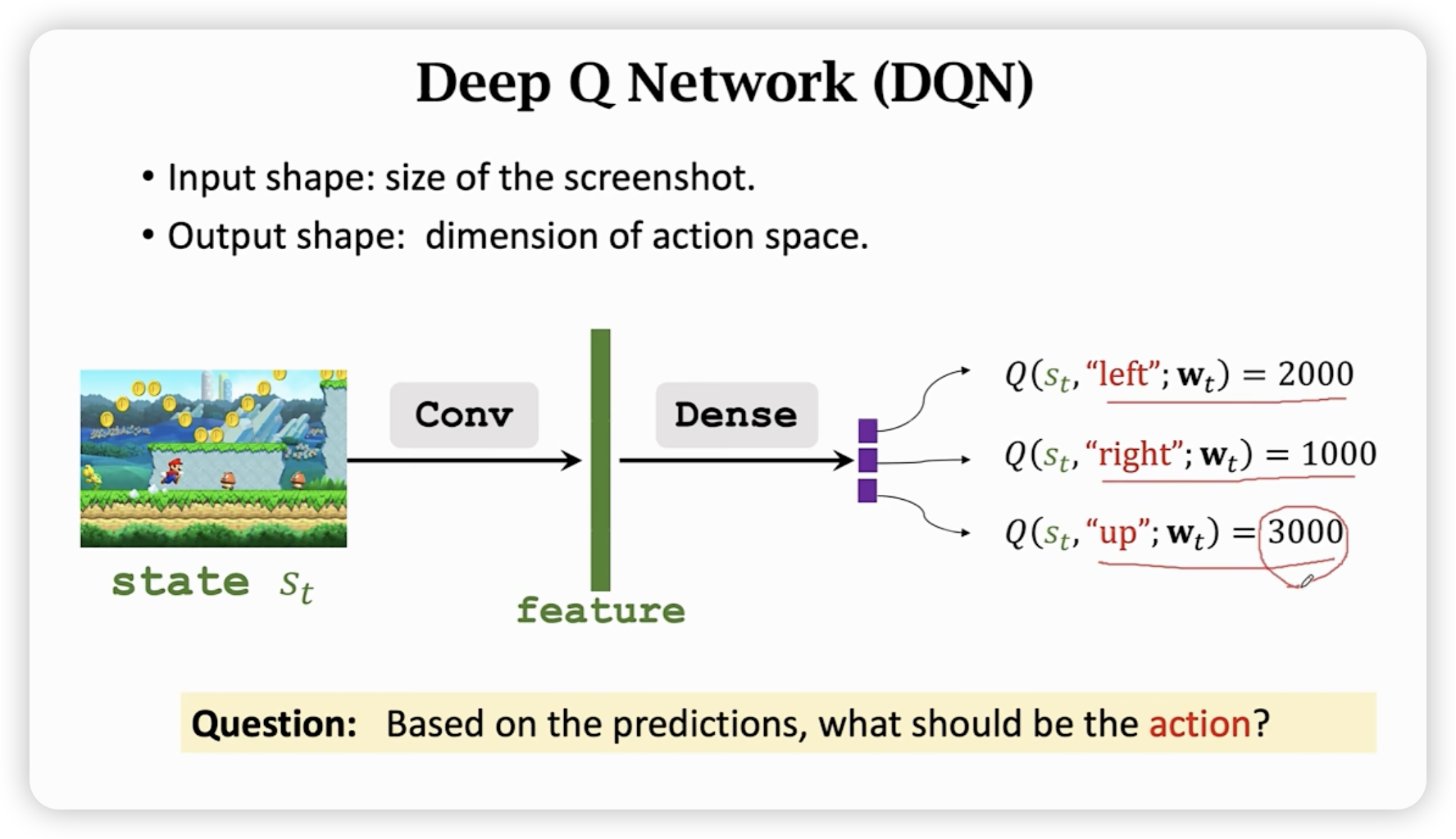
训练好网络后，就可以利用网络来决策最好的action。

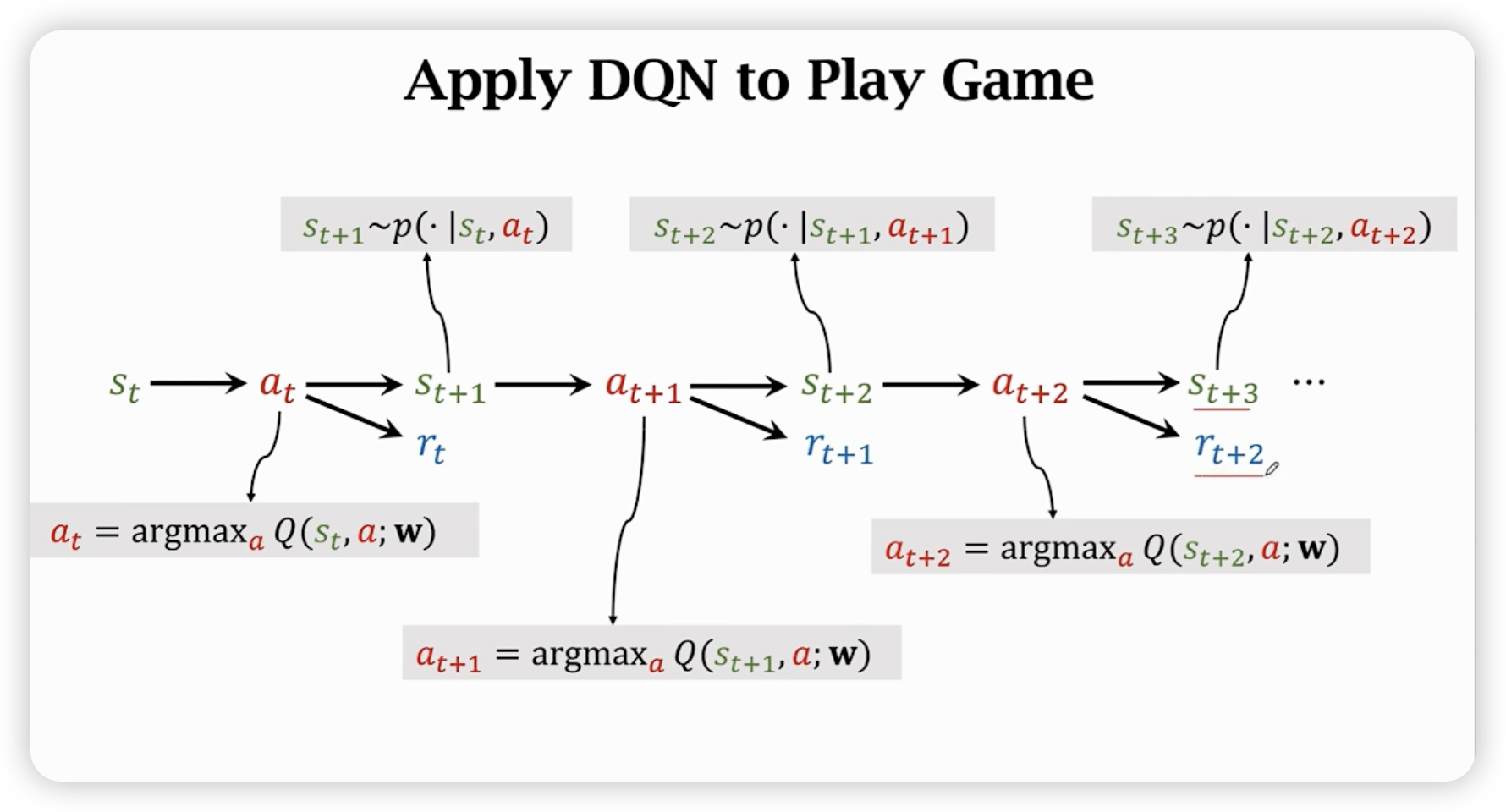
Temporal difference Learning

TD target: 用一部事实cost + 估计cost，随时间越来越准确。

这样在每一个时刻都可以用来算梯度更新模型参数。(不需要打完整场游戏就可以更新TD参数)

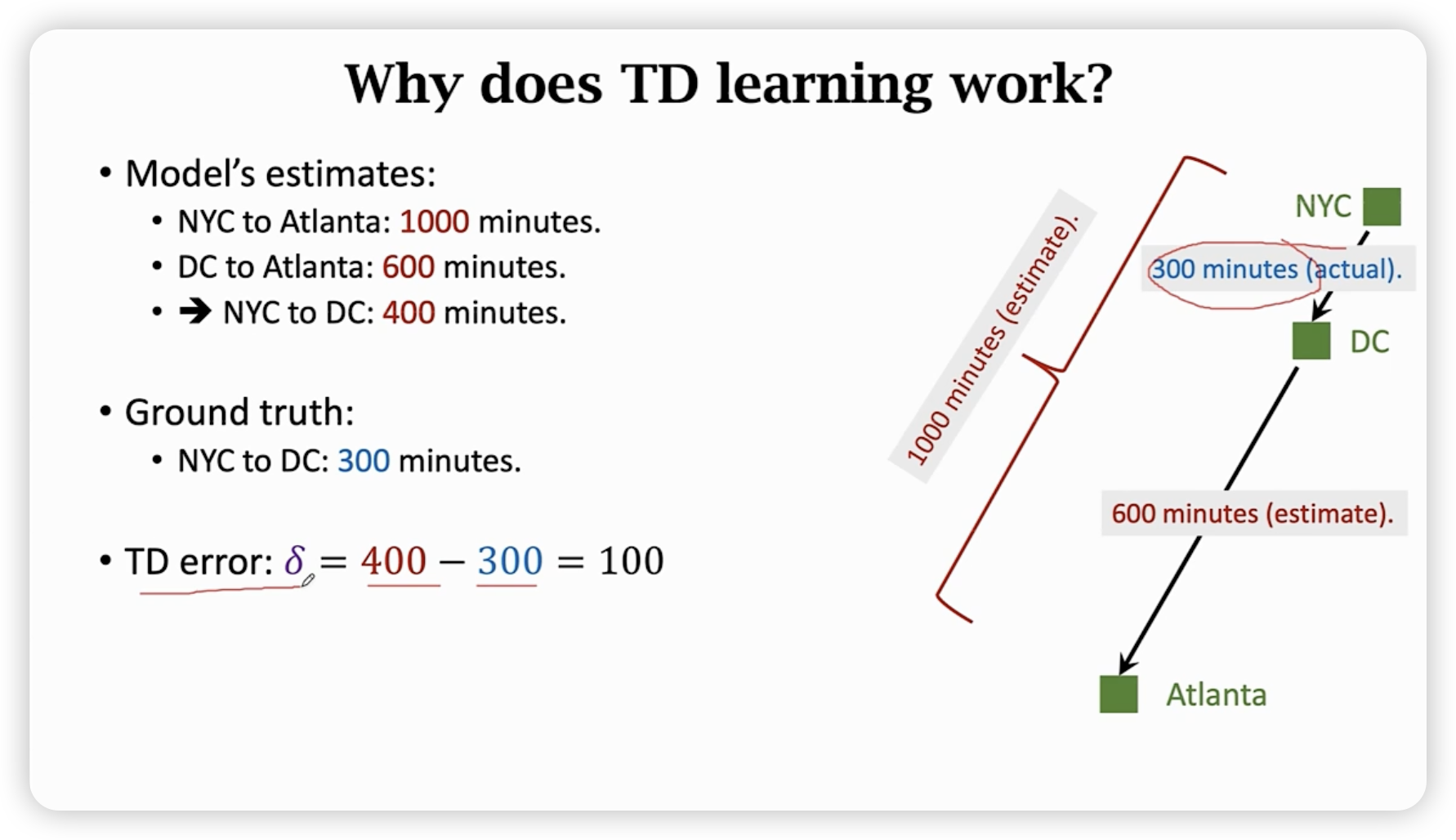
实际上是用梯度下降来减少TD error。

Apply TD Learning to DQN

我们知道$U_t$有这样的式子关系：

$U_t = R_t + \gamma\cdot U_{t+1}$

更形式一点，实际上，我们利用神经网络中打拼$W_t$，然后通过计算TD target计算理应更精确的W_t^'，利用这个loss对参数进行更新。

迭代过程

梯度算出参数和loss的关系，具体多了还是少了，由预测的$W_t$和理应的W_t^'的差异决定。

Policy-Based Reinforcement Learning

用神经网络近似策略函数$\pi$。

策略函数的定义：(注意$pi$是一个随机变量，每次是一个抽样)

我们需要一个神经网络来近似这个策略函数$\pi$。

在超级玛丽游戏中，我们可以用卷机网络来提取特征。

---

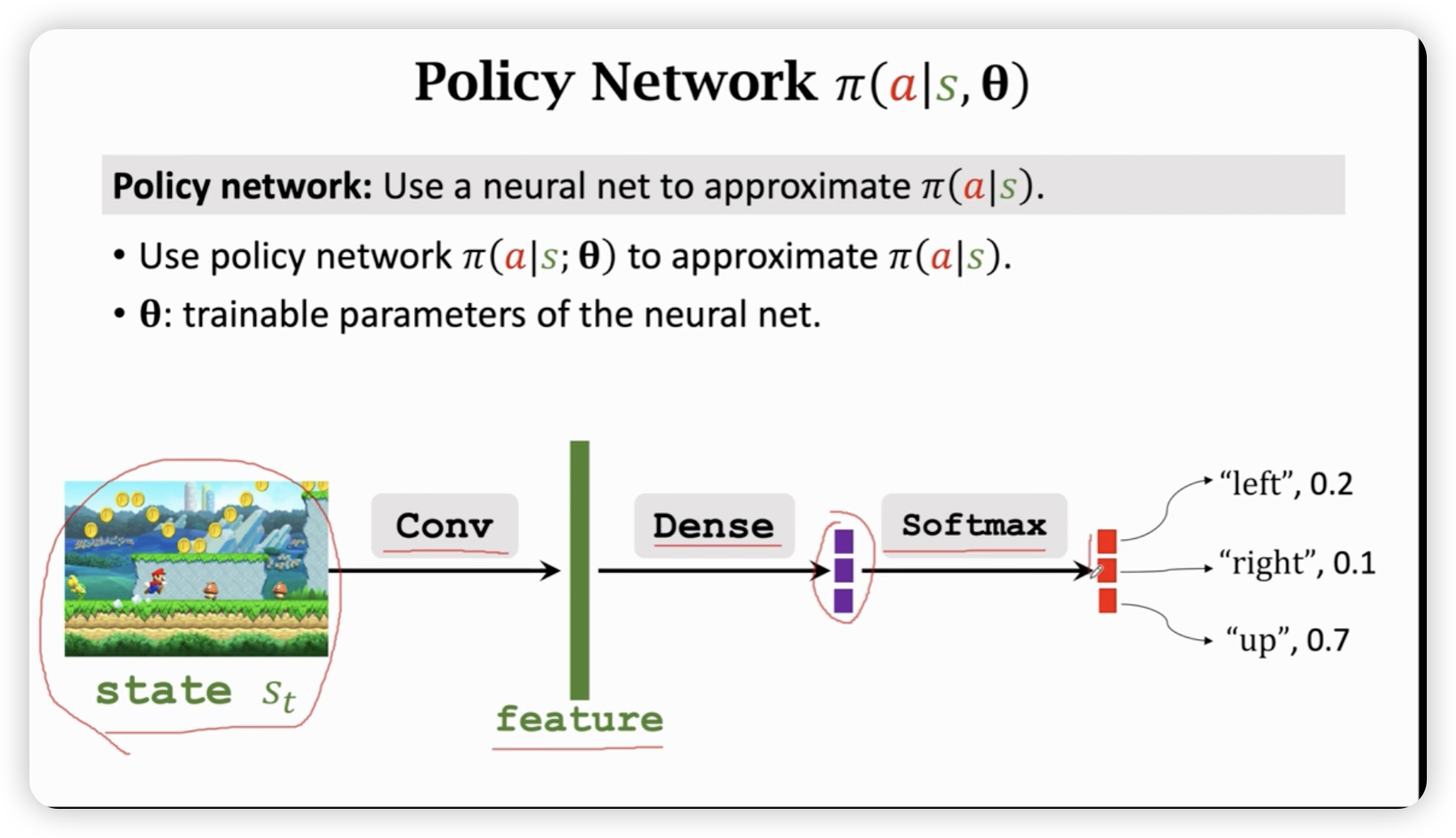
实际上，我们运用神经网络近似策略函数$\pi$，然后当作权值去加权$Q_{\pi}(s_t,a)$，得到近似的state-value function，最后我们希望这个state-value function最大，于是我们用梯度上升法去更新神经网络的参数。

在一个状态中，沿着让这个状态的state-value function变大的方向走，和随机梯度上升算法类似。

一些关于策略梯度的数学推导：

还可以做一个变形：

再依据具体问题离散与否，可以得到不同的策略梯度算法。

• 离散的时候
  

• 连续的时候

无法直接算积分，故采用蒙特卡洛近似。（就是抽样很多随机样本，无偏估计，对离散时候同样适用）

但是使用蒙特卡洛近似需要的一个期望（也就是一个权值分配），我们采用第二种变形变出来一个权值分配，于是就可以使用蒙特卡洛近似了。

迭代Algorithm

这里埋了一个雷，$Q_{\pi}(s_t,a_t)$不知道怎么求，有两种办法。

第一种方法是抽样完一次游戏，暴力去算。

第二种方法是再用一个神经网络来近似$Q_{\pi}(s_t,a_t)$，也就是actor-critic算法。(将价值学习和策略学习结合起来)

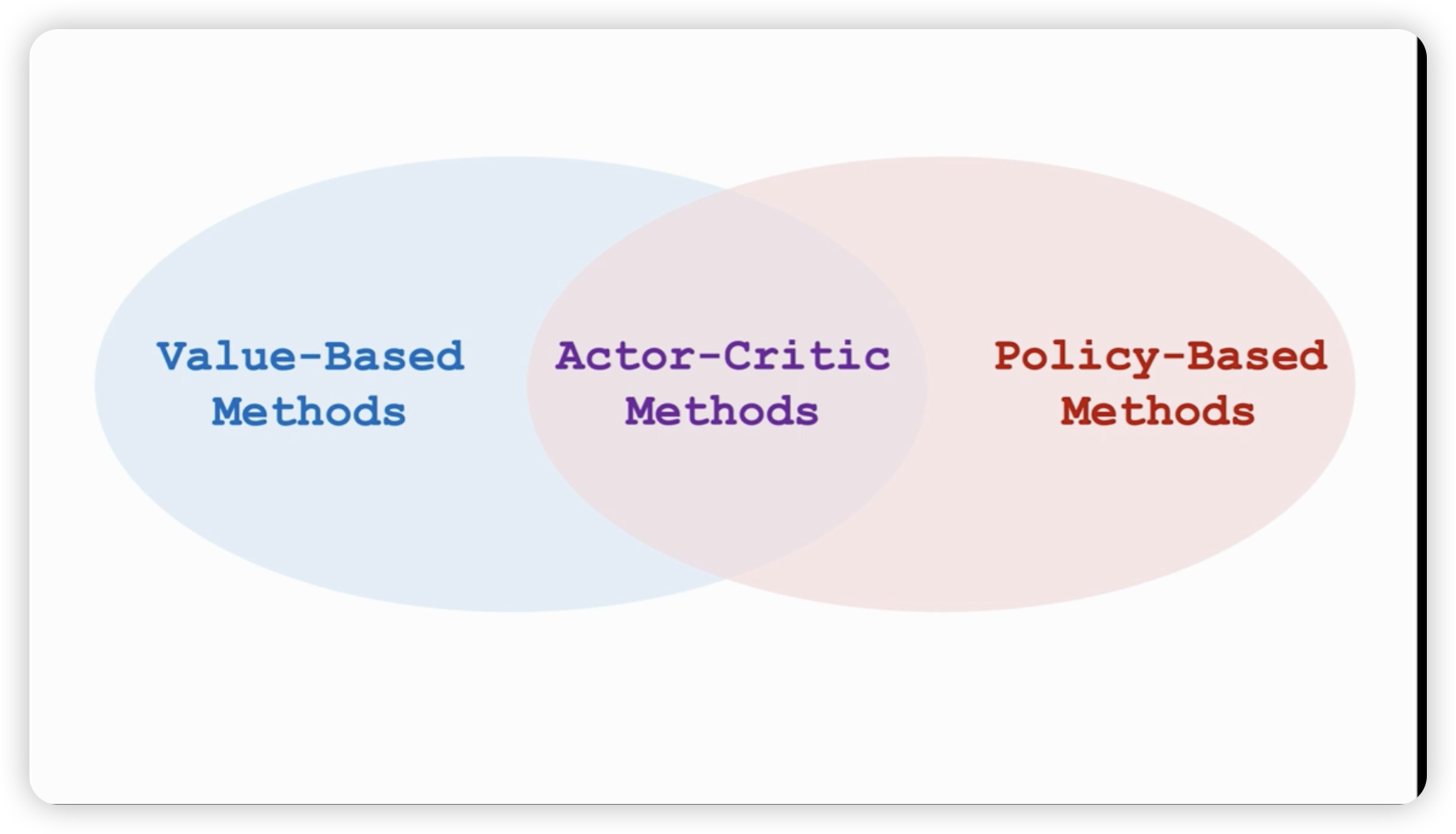
Actor-Critic Method

两个神经网络，一个负责运动，一个负责打分。（通过环境来学习这个网络）

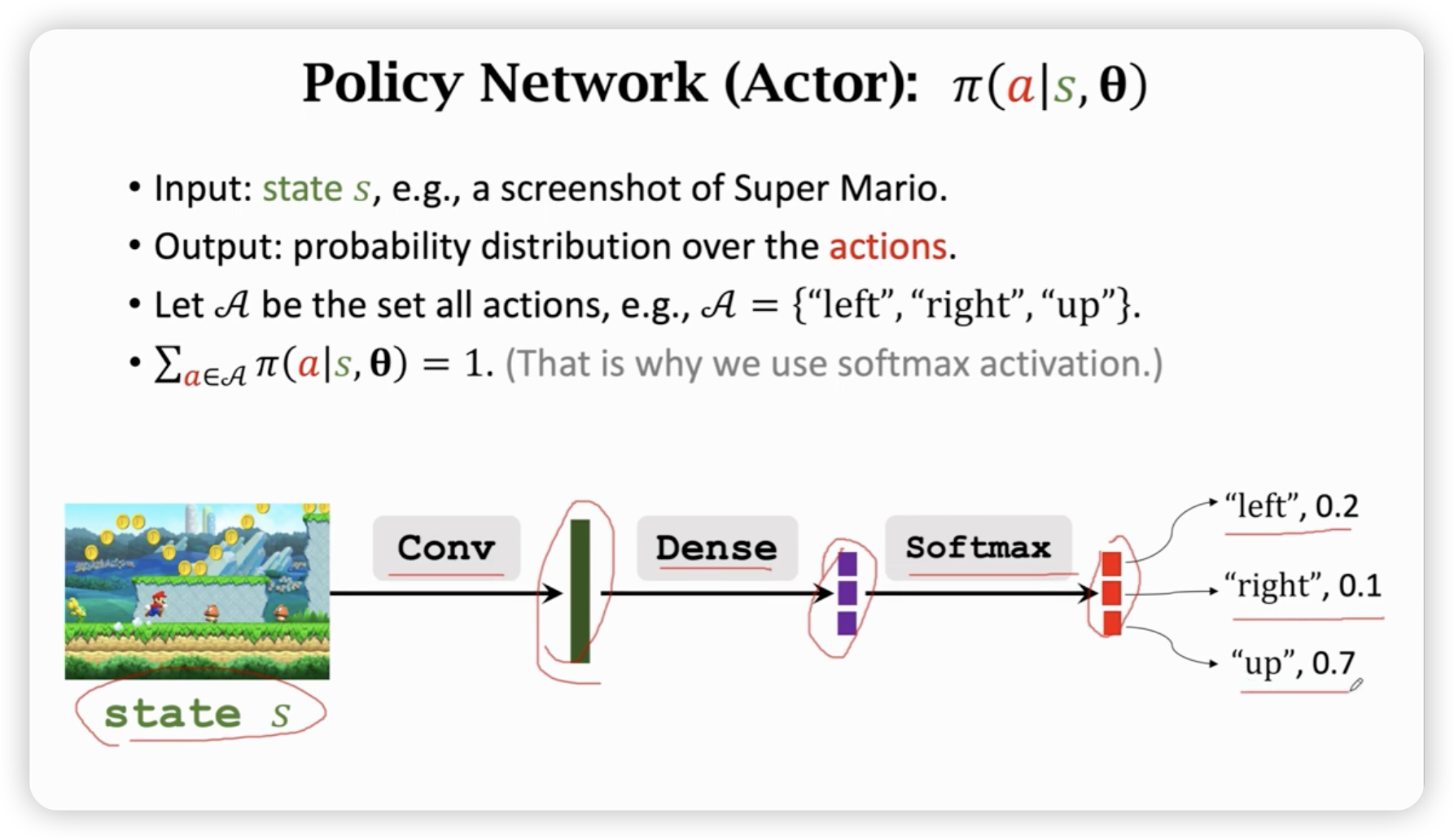
我们希望估算$V_{\pi}(s)$，但是定义式的两个东西我们都不知道，于是我们用两套神经网络分别来近似这两个东西。

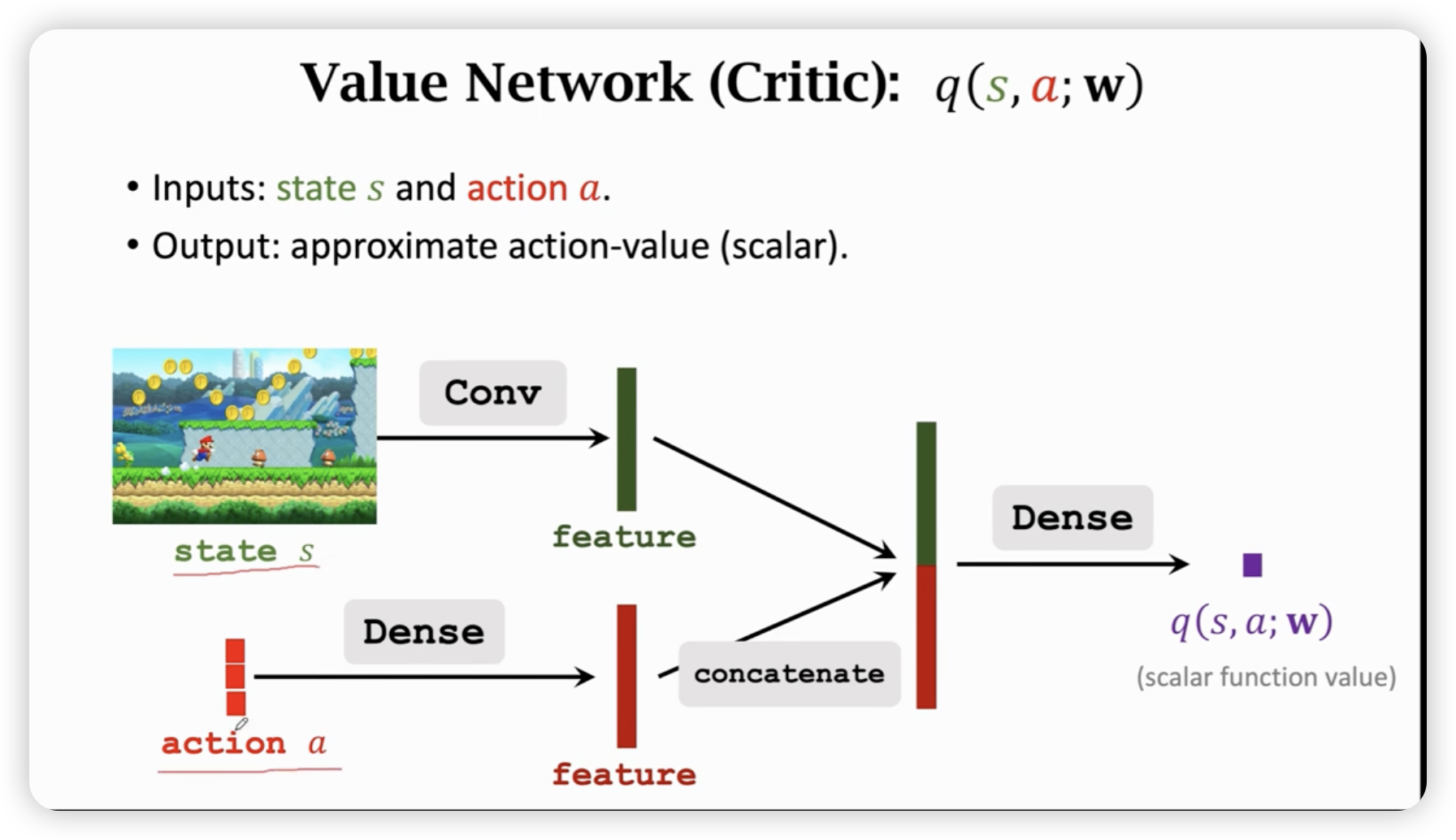
Train

策略网路依赖critic网络，critic网络依赖环境奖励。

一些具体的细节：

Update value network using TD

Update policy network using policy gradient

总结一下：

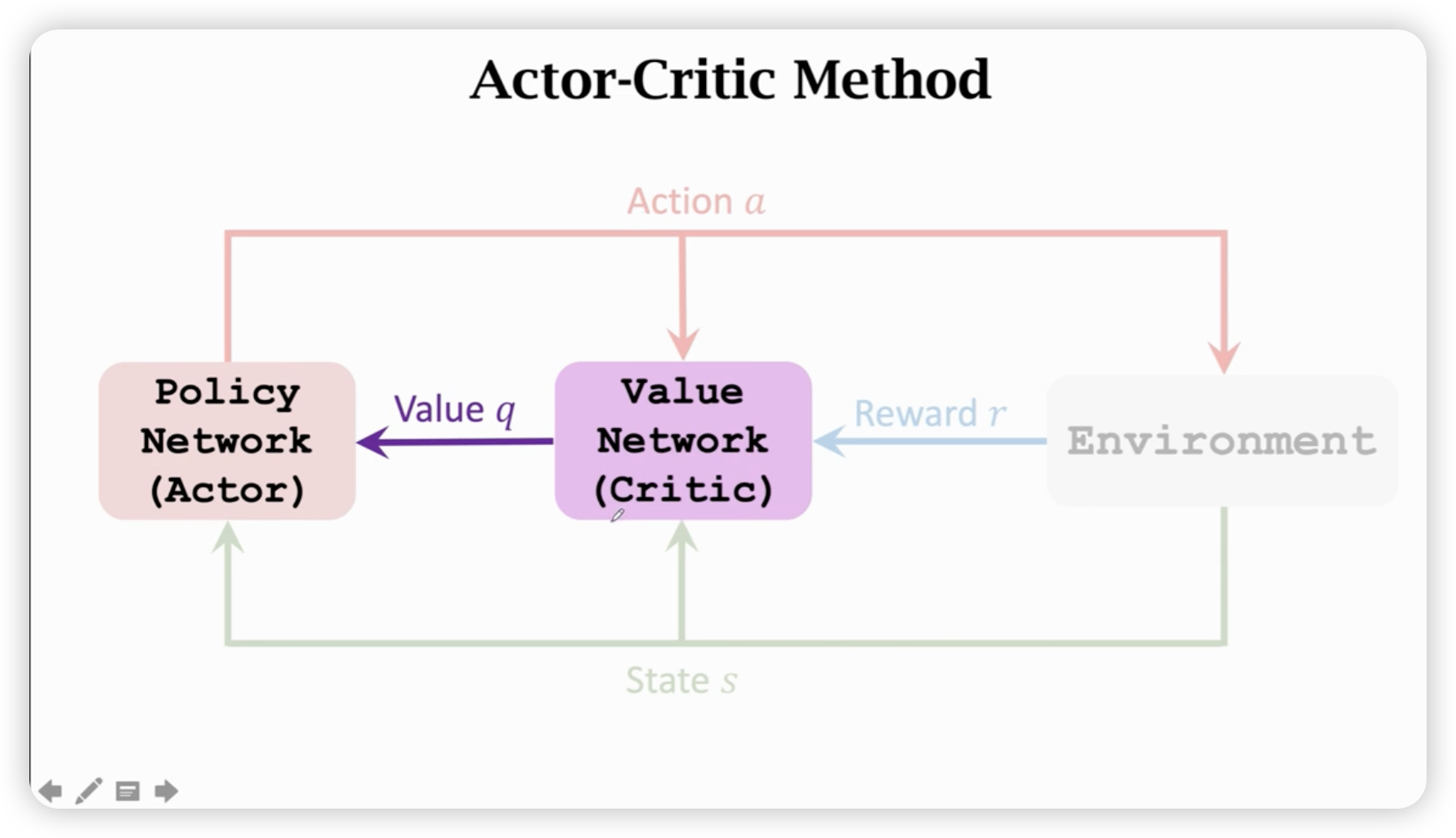
Thus, one iteration is like this:

每一次迭代都只做一次动作，更新一次参数。（其中用了多次蒙特卡洛近似）

其中，如果把第九条的$q_t$换成5条中的$\delta_t$，其实期望结果没有变，但是方差变小了，收敛速度会有提升。

---

训练结束，学习完成后，就不需要裁判了。

---

policy network提高决策你表现。

value network依据reword让评估更准确，用来帮助决策网络的优化。