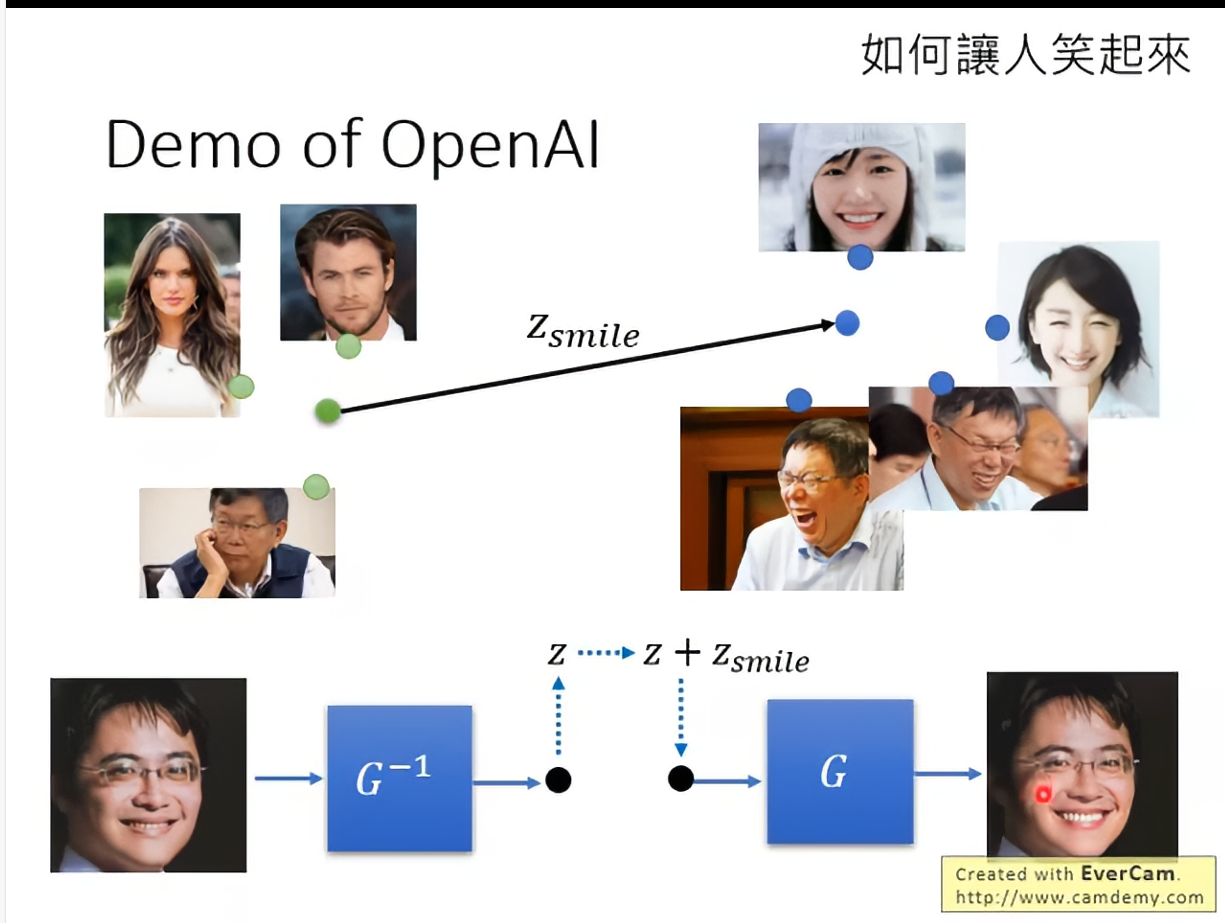
Deep Generative Model
Deep Generative Model
PixelRNN
很朴素的想法,就是用RNN来生成图片,每一个像素点的生成都是依赖于之前的像素点。也是做一个自回归unsupervised learning。
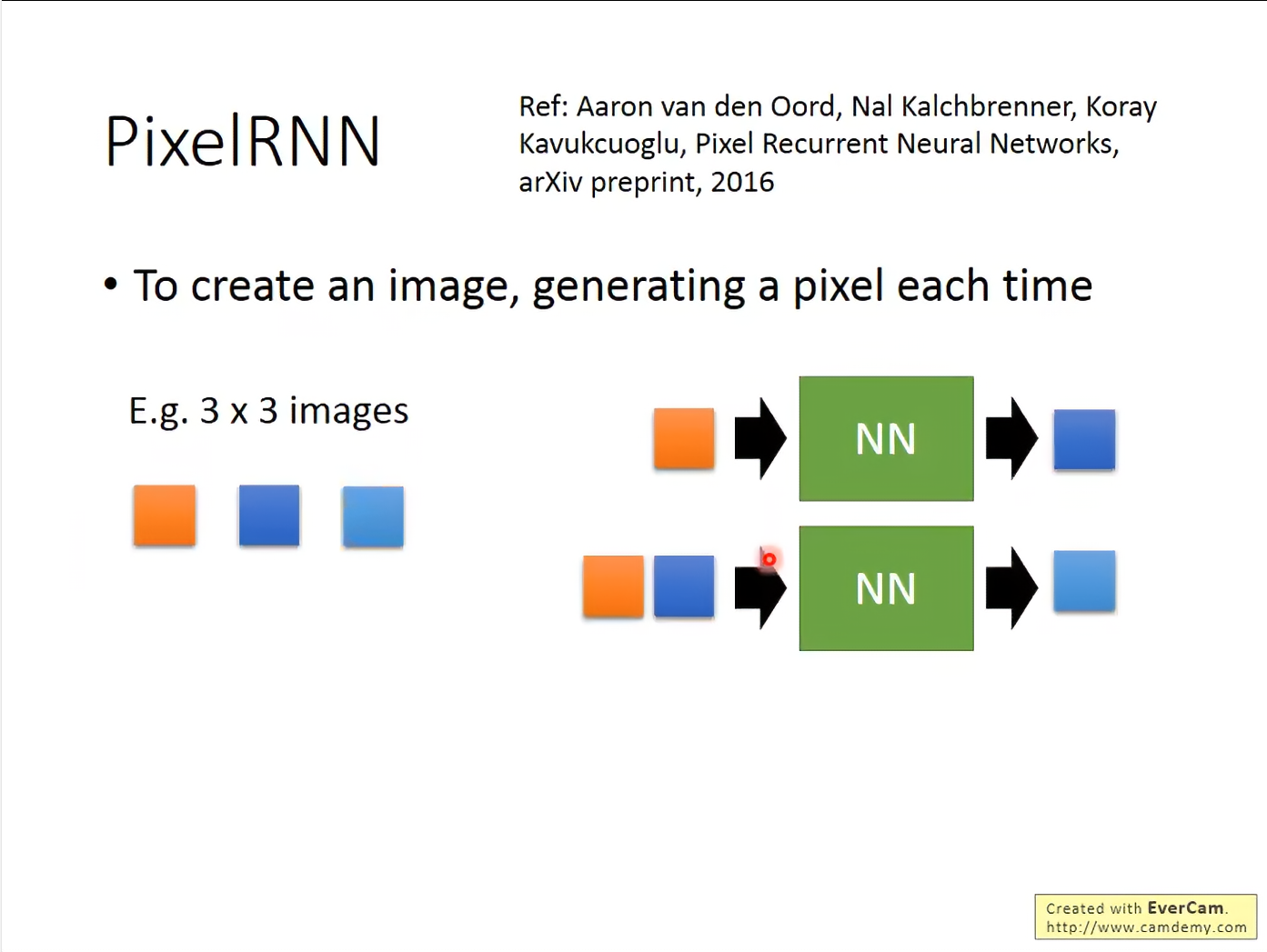
结果不好,且慢。
VAE(Variational Autoencoder)
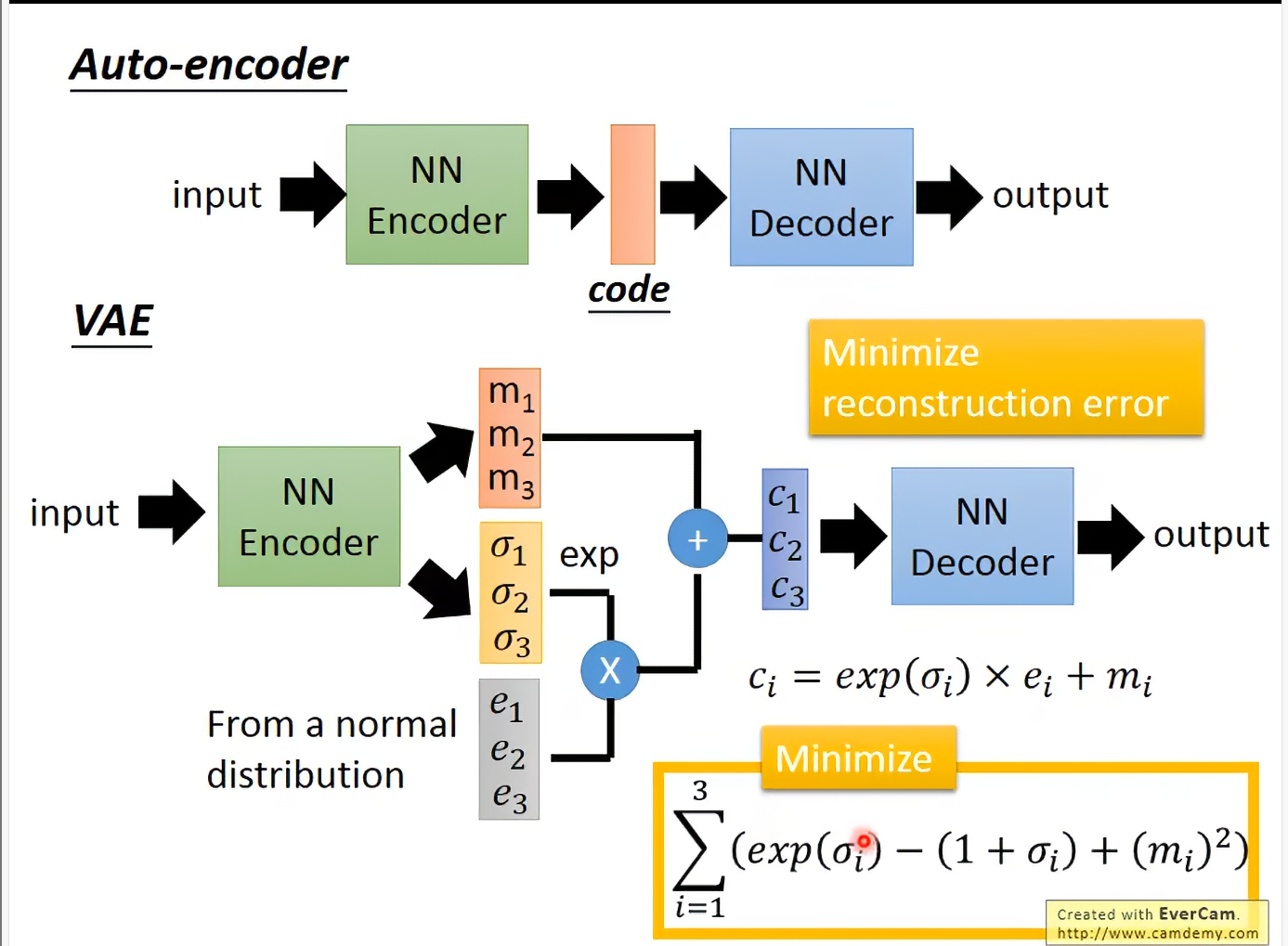
为什么用VAE?
Intuitive的理由:
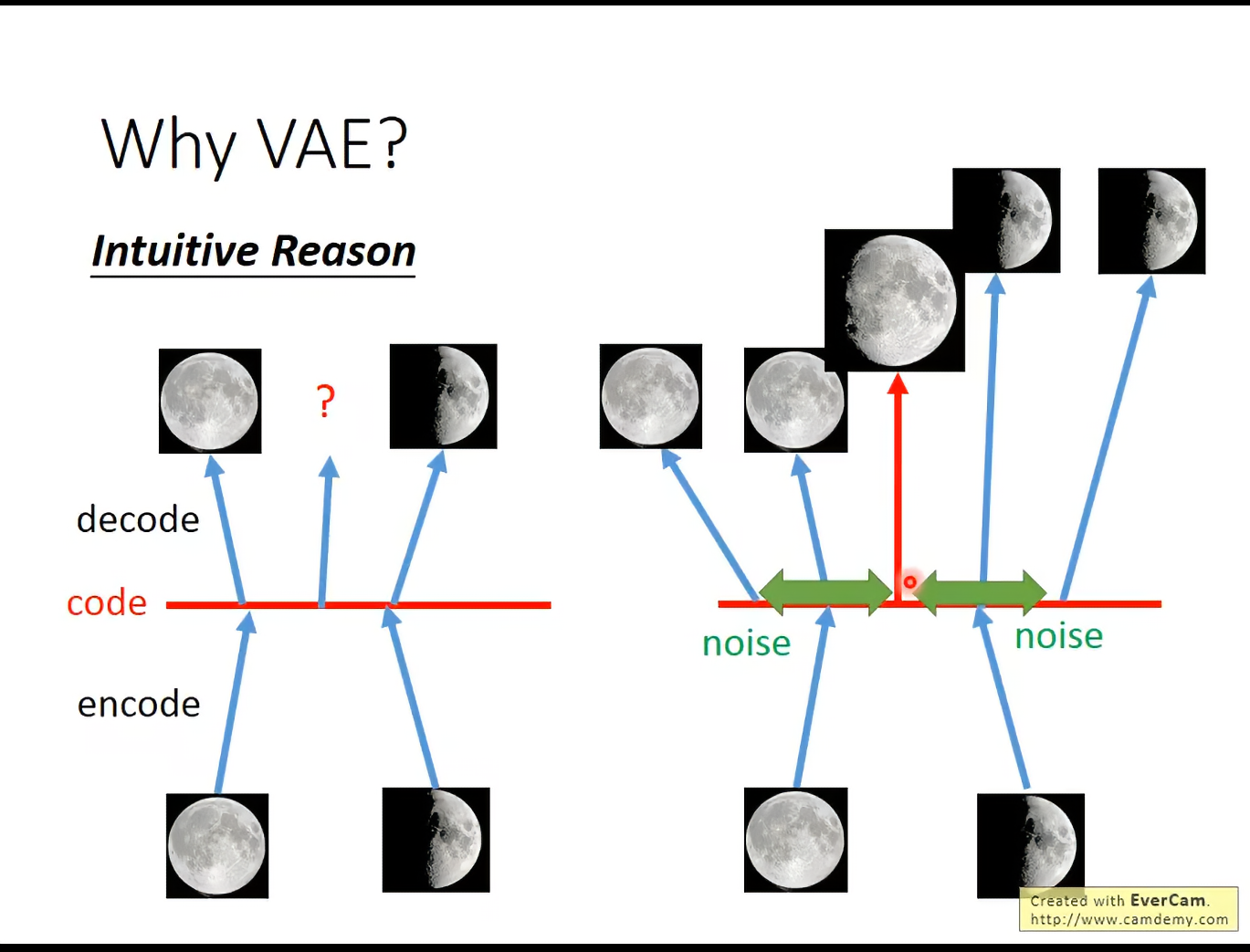
VAE通过引入Gaussian,使用noise让模型更鲁棒。VAE在minimize时会考虑与之相近的图片。因为noise的引入让embedding space更加平滑。在code space随机sample会比在Auto encoder中更加有真实。
exp保证noise强度都是正的,当做variance。
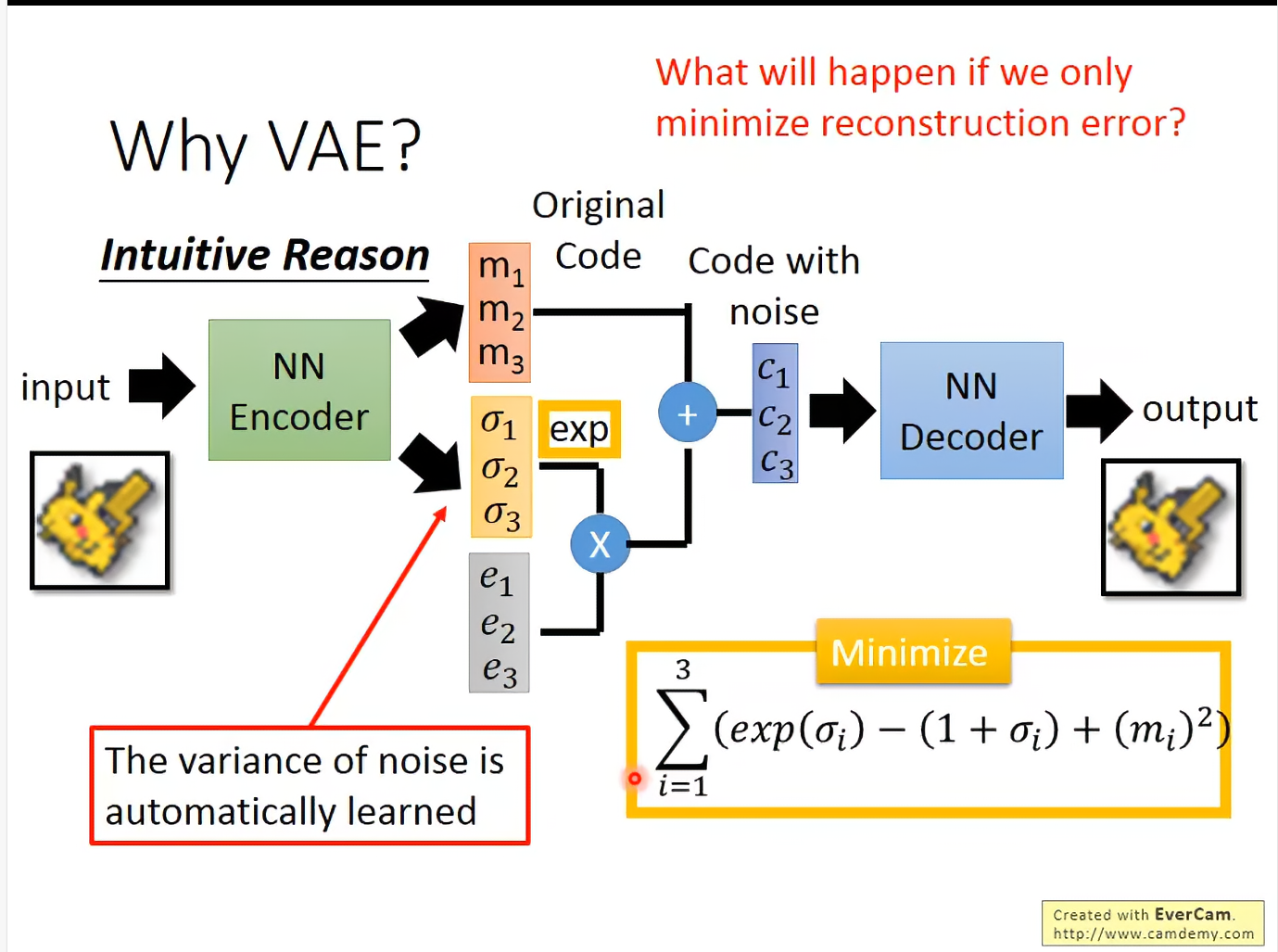
但是直接这样train不行,因为这里是模型自己learn的,当然给最好(退化到AE,不会有image overlap情形)。
注意这里加上了正则项的限制,在这个限制中取0(此时对应的噪声强度为1)时,正则项最小,避免往负无穷跑
那项相当于一个L2正则项,让code space更加sparse,更不会overfitting。
当然这个正则式不会只有上述heuristic的理由,还有一些理论上的证明:
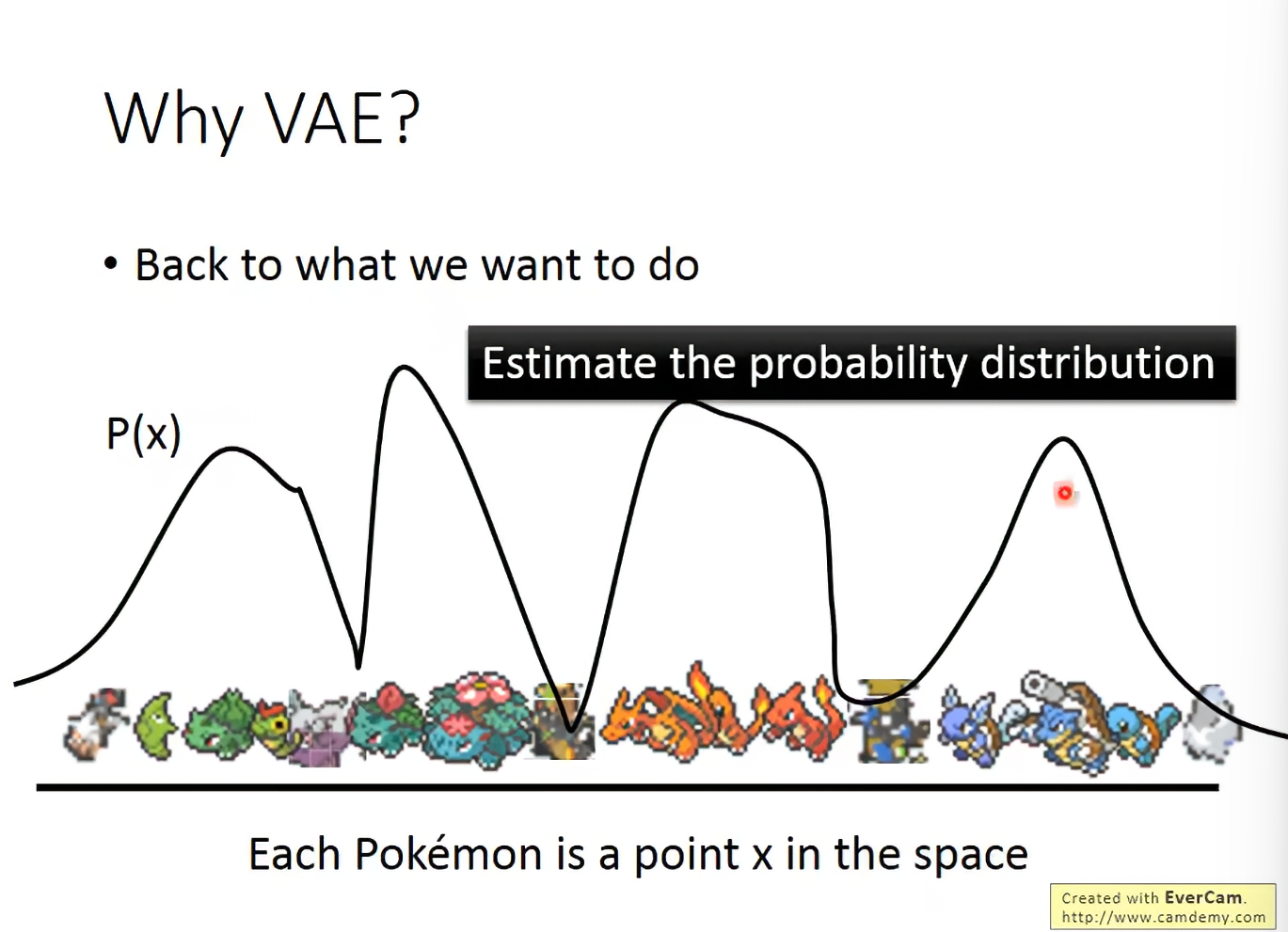 每个image都是高维空间中一个点,其实我们就是要取估计这个P(x)的分布,找到后就直接sample就行了。
每个image都是高维空间中一个点,其实我们就是要取估计这个P(x)的分布,找到后就直接sample就行了。
Gaussian Mixture Model
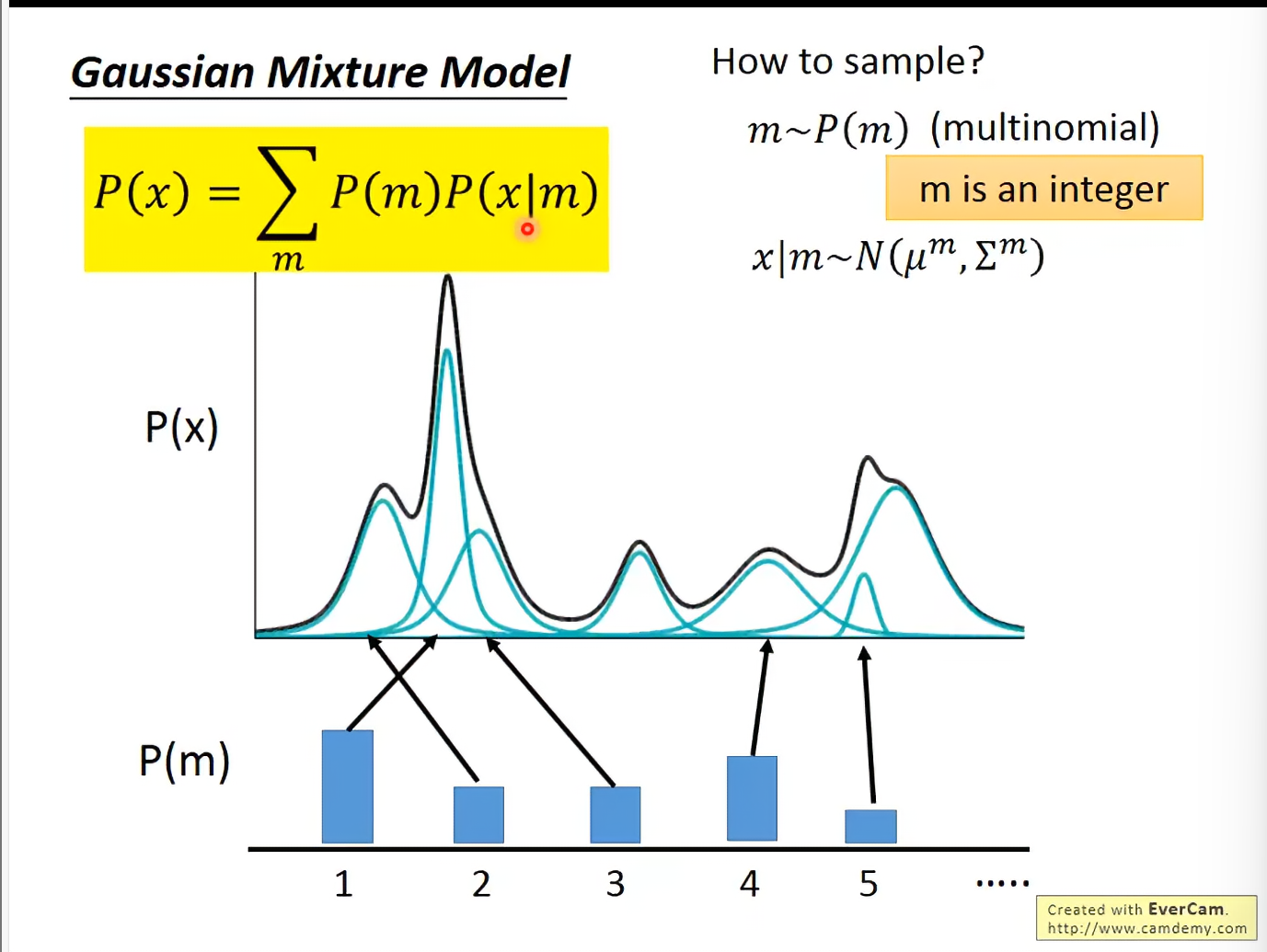
sample process : 先抽一个确定的gaussian,然后再从这个gaussian中sample。
如果知道了mixture的数目,再结合数据,就可以用EM Algorithm来估计每个gaussian的参数。这里每个gaussian更像是生成过程中对象的一个特质vector,而不是简单分类cluster。
VAE其实就是Gaussian Mixture Model的一个distributive representation的版本。
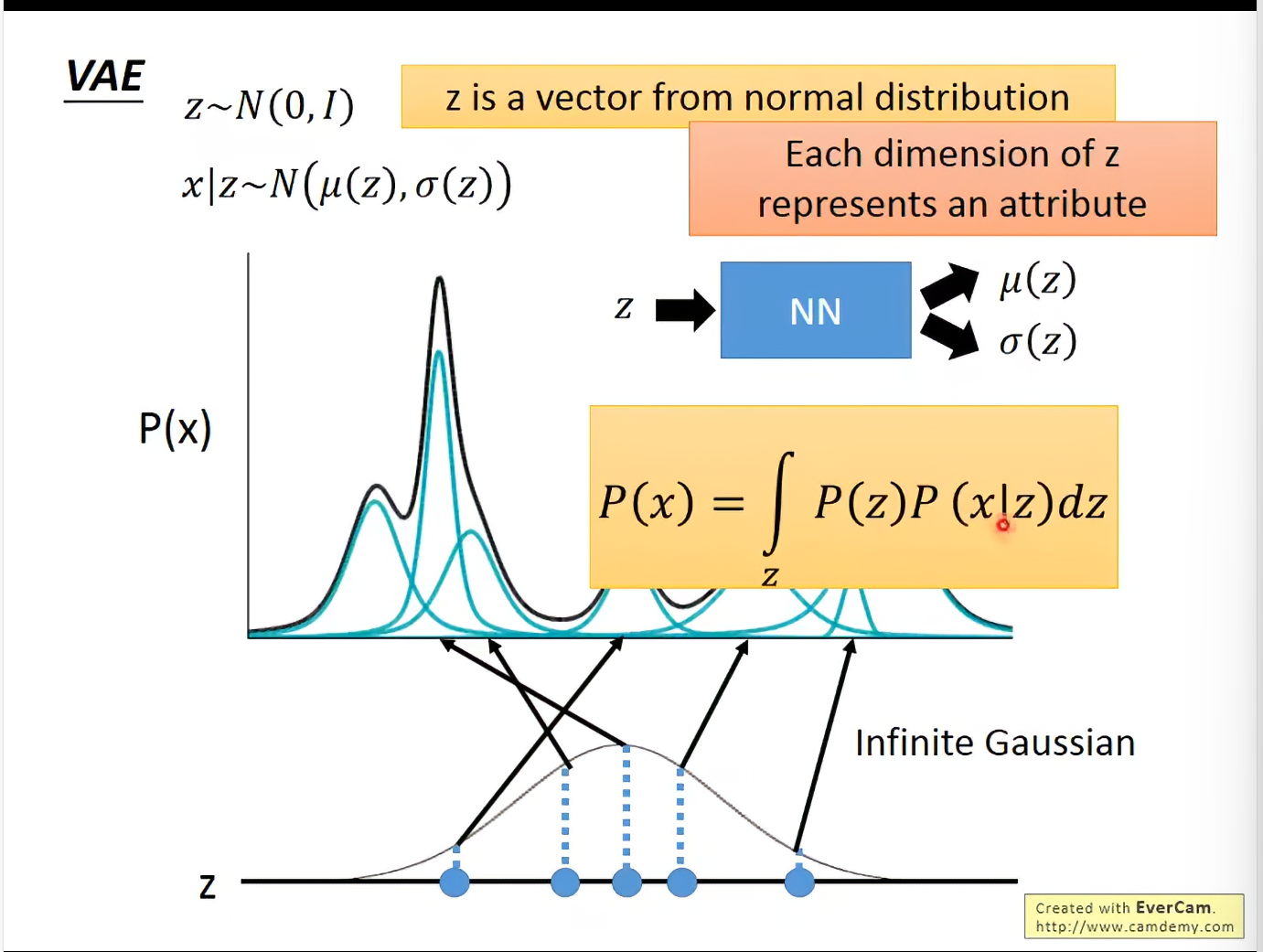
当然z不一定是gaussian,也可以是其他的分布。在各个特质独立且权值有重要的少trivial的多情况下,采用gaussian也是合理的。
于是就可以用Maximizing likelihood来训练的参数。
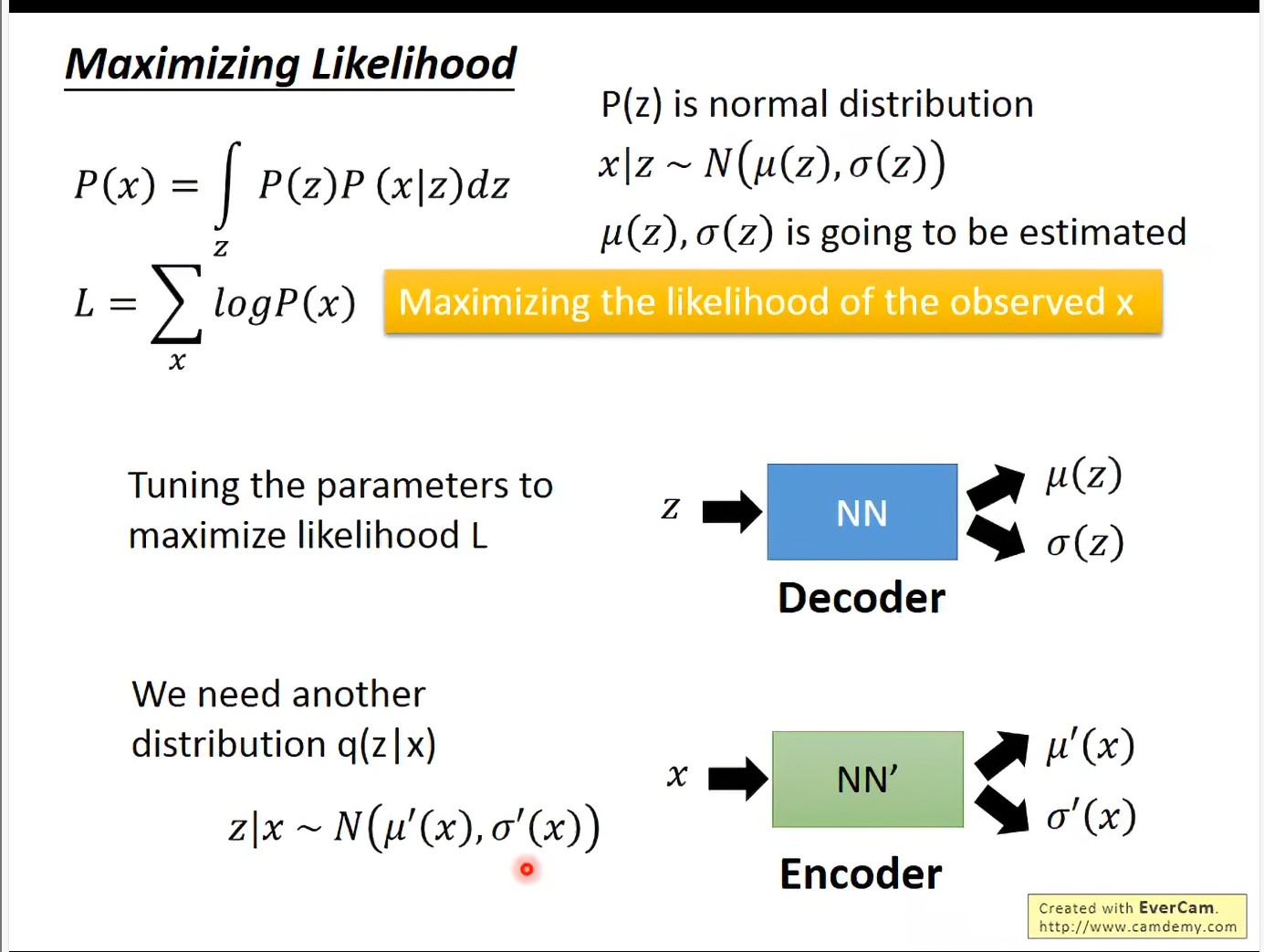
我们又反过来定义了函数
注意到一下式子推演:

本来我们要找的是让likelihood越大越好,现在我们要找来maximizing 这个下界。(又是一个把最优化问题变成最优化估算下界的问题)
为什么要引入,是为了解决lowerbound升不一定主函数会升的问题。
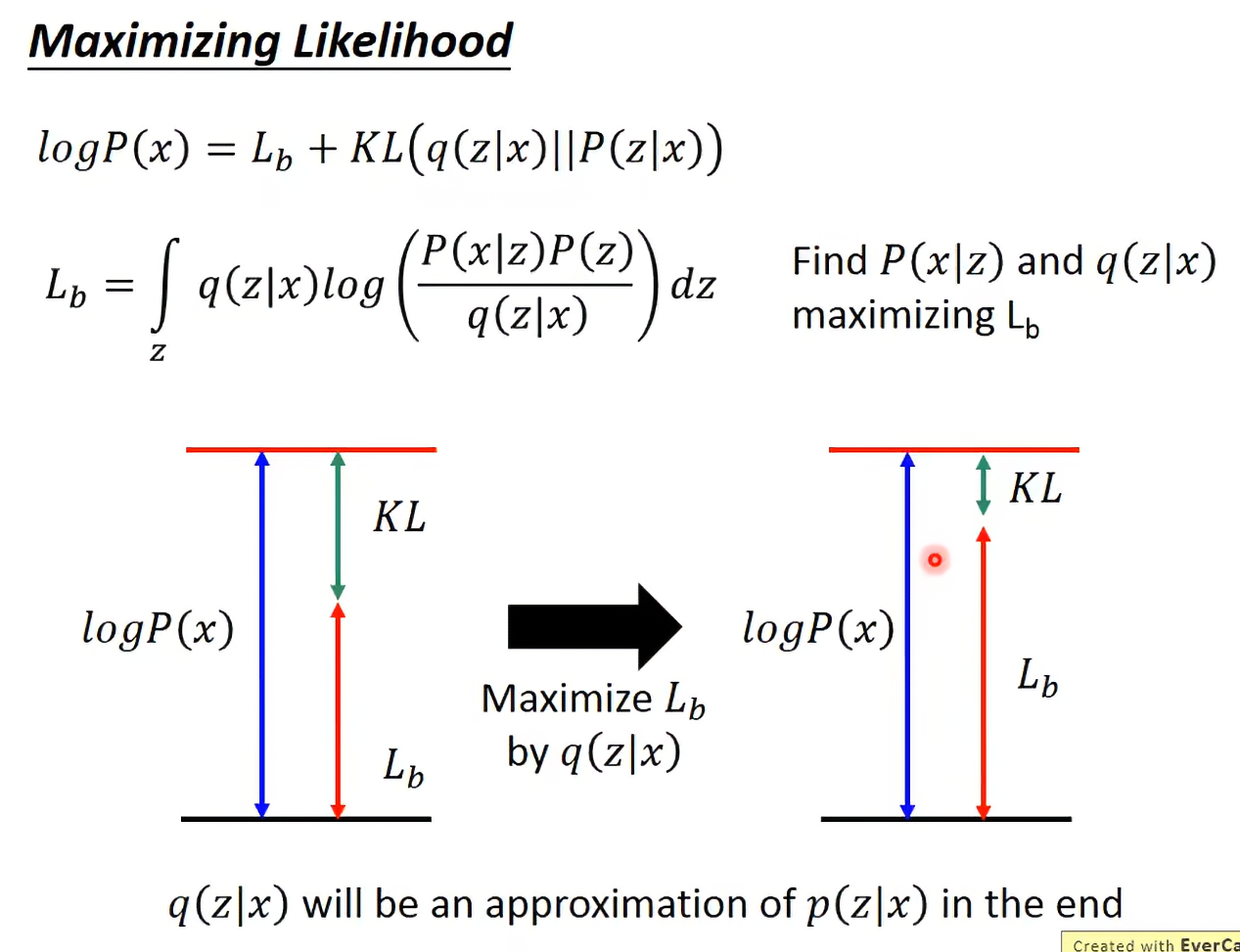
因为q和P没有关系,所以调整q不会影响蓝色的,所以我们固定住P,调整q,让下界最大化的同时KL绿色部分缩小(因为红色与蓝色总和为固定值蓝色)。这样可以让下界更贴近真实的likelihood。当KL散度为0时,下界就是真实的likelihood。这时如果你能提升这个下界,就是提升了likelihood。
同时我们有一个副产物,顺便会找到q与P十分相近的解!
继续推导:
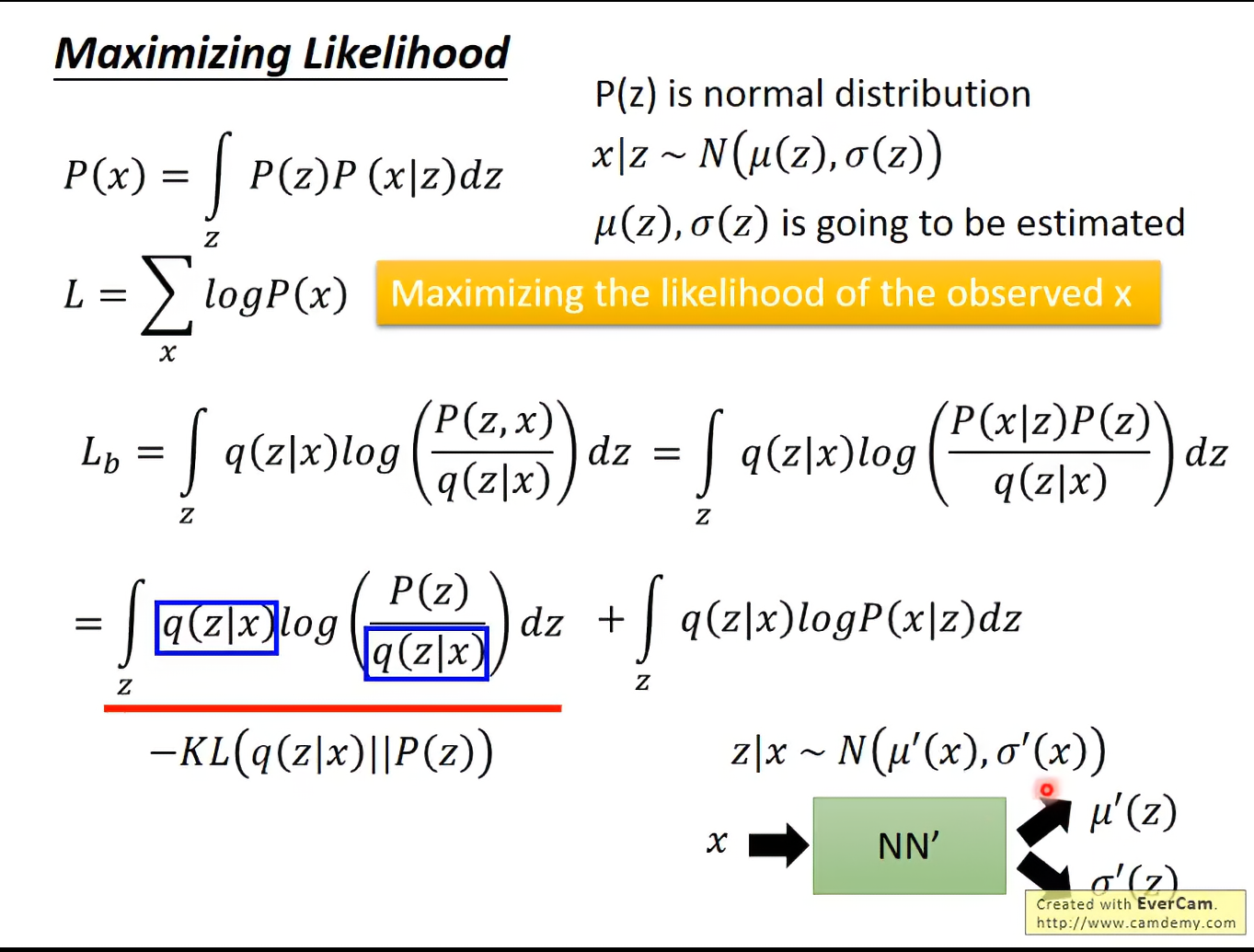
因为q是自己定的函数,我们也用nn来拟合gaussian分布。
这里对于KL,我们的任务就是去调整VAE网络框架一开始的参数,来让更接近我们一开始假定的标准正态分布。
具体的数学过程参见论文,最后的结果就是最开始说的那个intuitive regulation的式子。
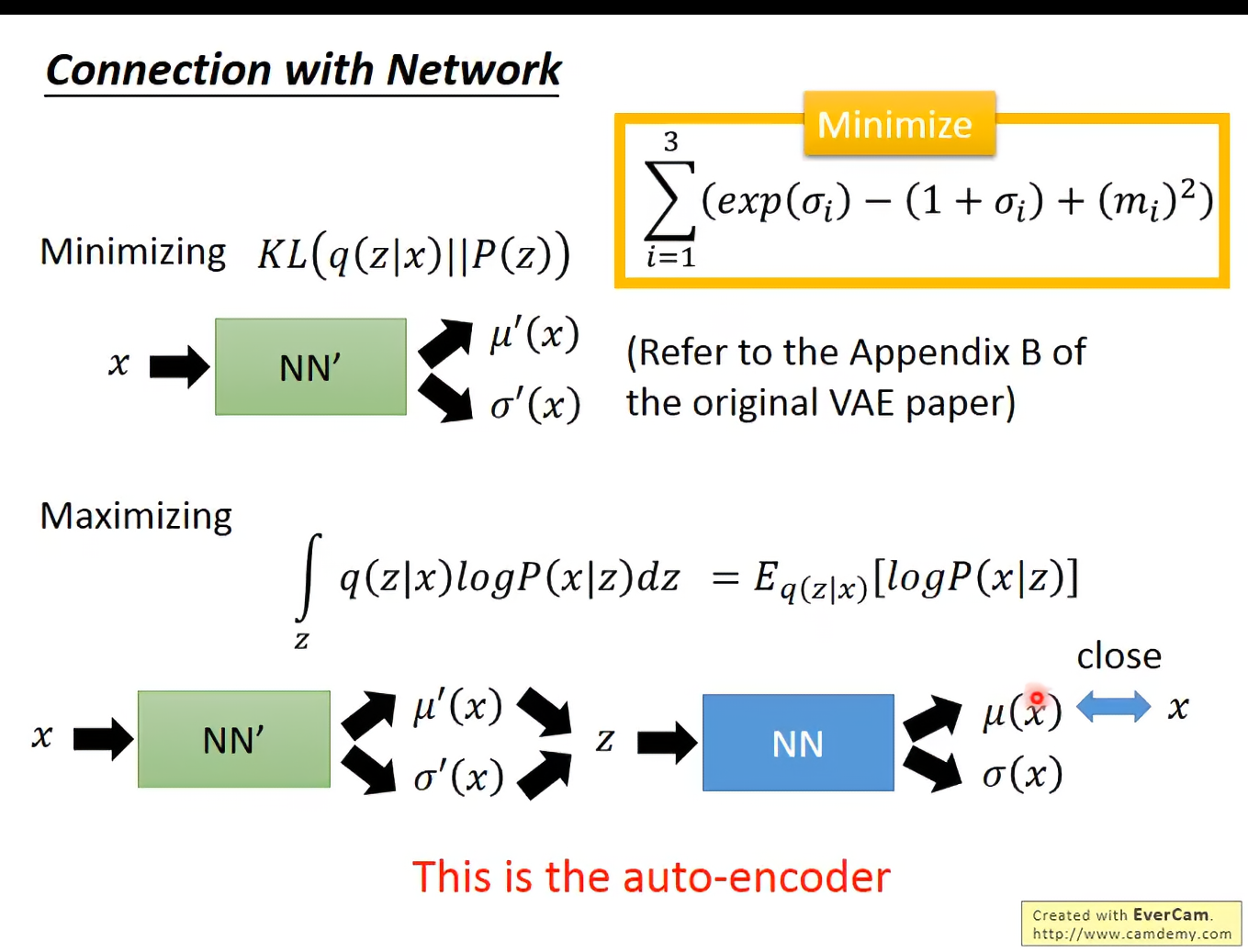
这两项合起来就是我们在一开始看见的VAE的loss function。
Problem of VAE
VAE其实没有在做generate而是在逼近数据集,只是在模仿。

所以接下来就有GAN。可以看我之前关于GAN的blog。
Flow-based Model
前文几种方法或多或少有些问题。

我们先解构一下生成器:
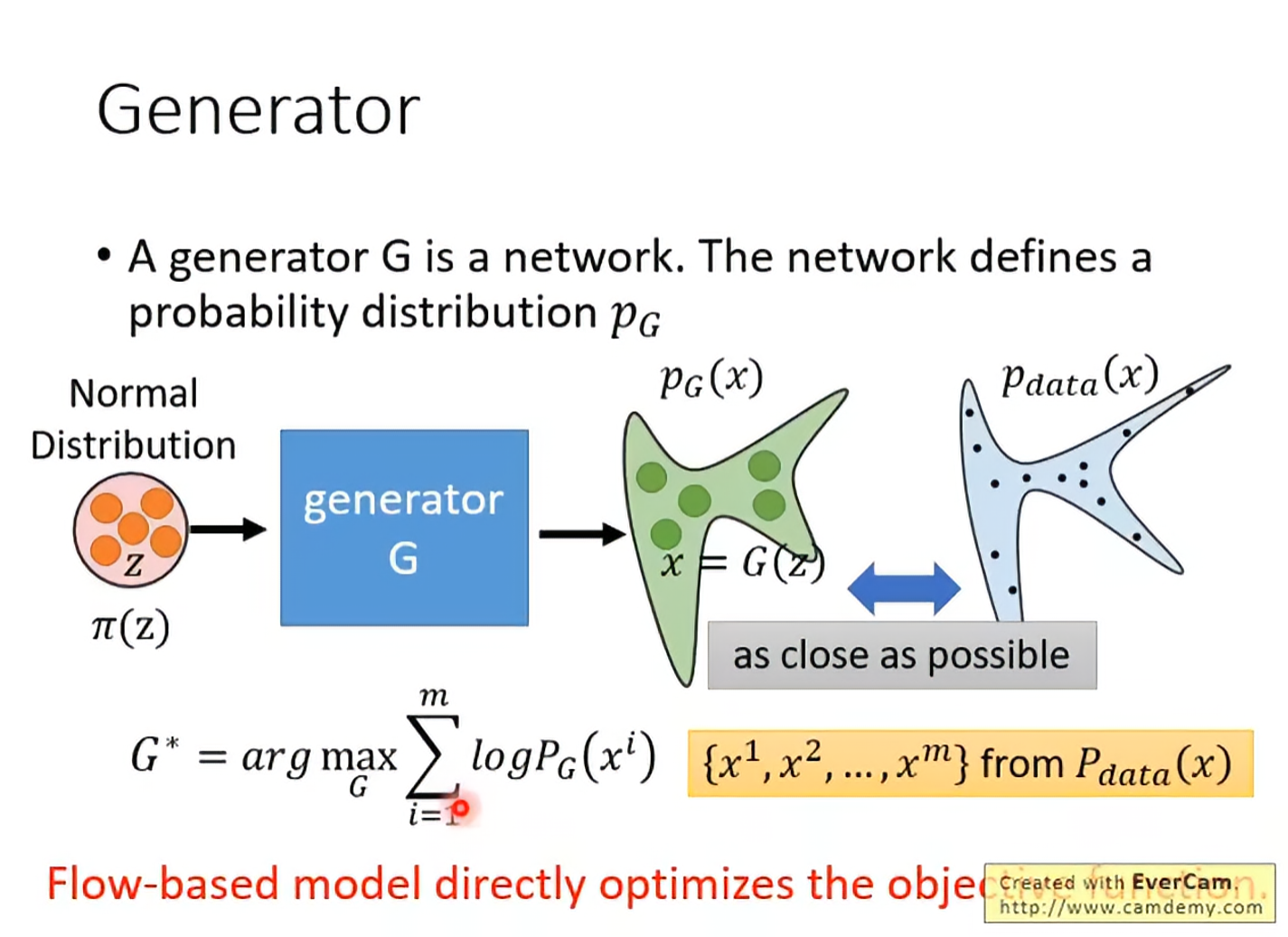
看flow之前需要干三件事:
Jacobian Matrix

注意到
更注意到上式的展开式中:多元情况下偏导数的乘积 $ \frac{\partial z_1}{\partial x_1} \cdot \frac{\partial x_1}{\partial z_1} $ 不等于 1。
在多元函数中,偏导数表示在固定其他变量时,一个变量对另一个变量的变化率。但是,由于变量之间可能存在相互依赖,单独的偏导数不能完全描述变量之间的关系。
在多元情况下,偏导数的乘积不一定等于 1,原因如下:
-
变量的相互依赖性: 在多元函数中,$ x_1 $ 可能同时依赖于 $ z_1 $ 和 $ z_2 $,而 $ z_1 $ 也可能依赖于 $ x_1 $ 和 $ x_2 $。
-
固定其他变量的影响: 当计算偏导数 $ \frac{\partial z_1}{\partial x_1} $ 时,我们假设 $ x_2 $ 固定;而当计算 $ \frac{\partial x_1}{\partial z_1} $ 时,我们假设 $ z_2 $ 固定。这两种情况下,固定的变量不同,导致结果不对称。
更一般地,偏导数乘积不等于 1,而是需要考虑其他变量的影响。
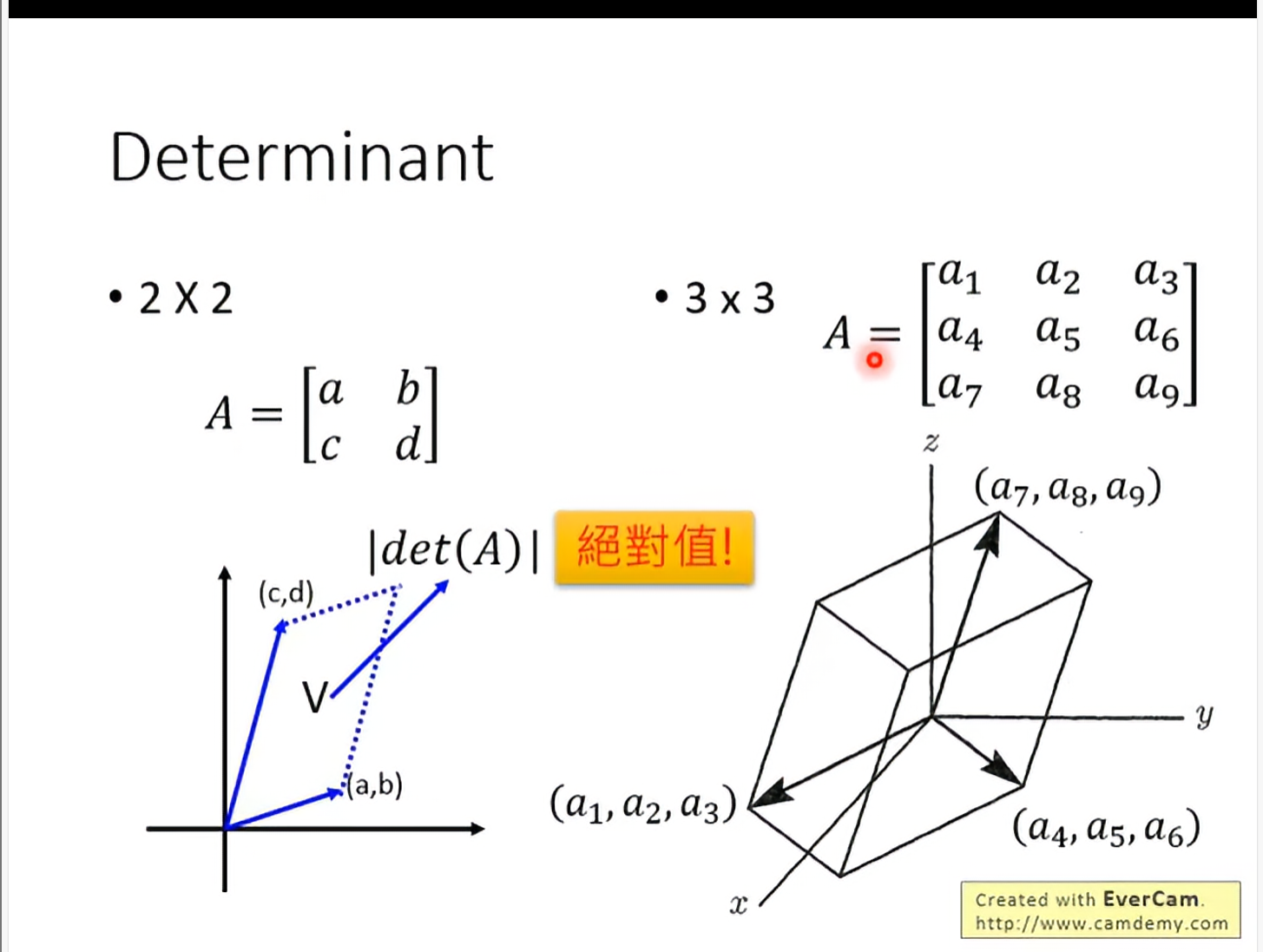
Determinant
Change of Variable Theorem
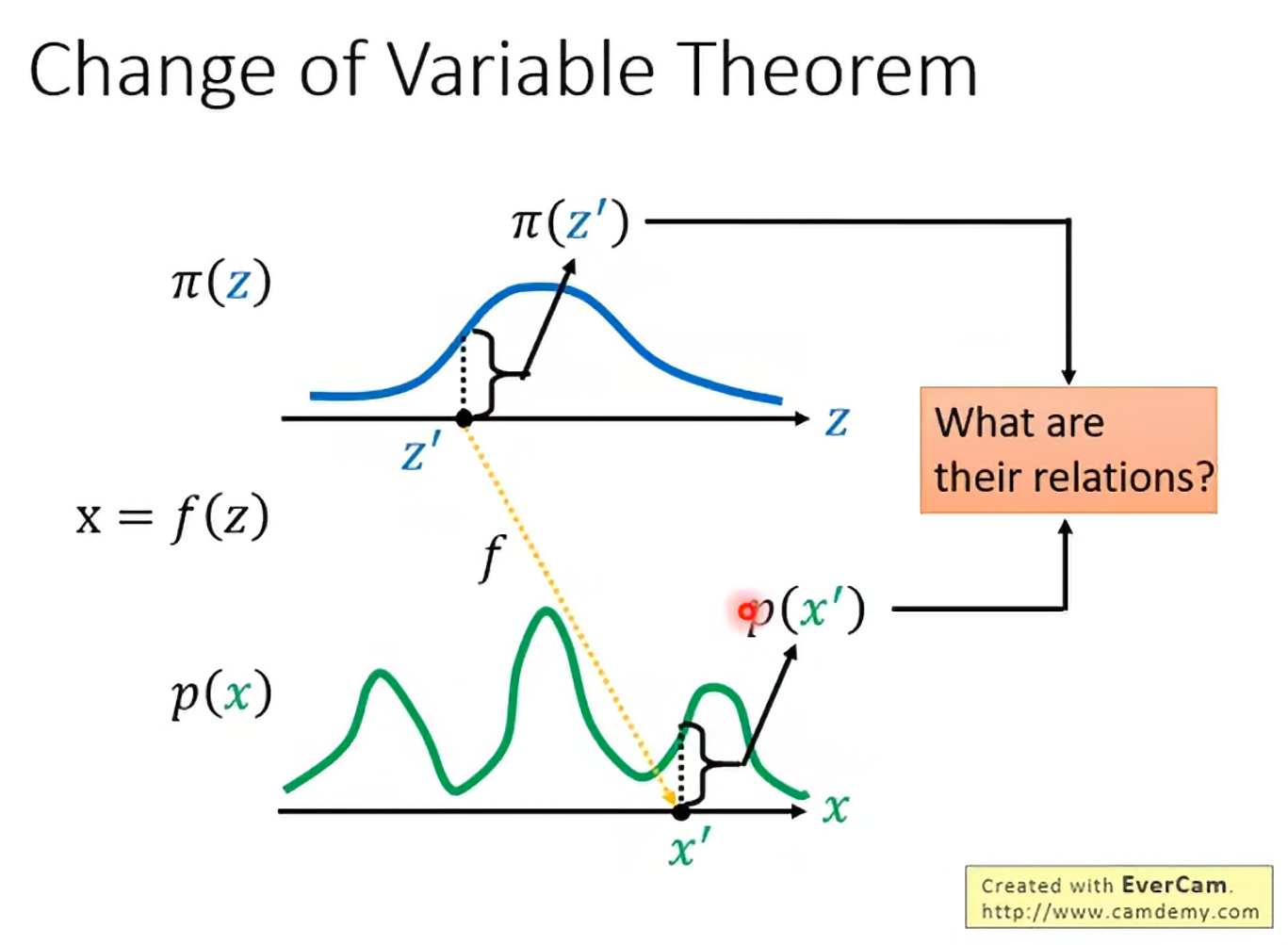
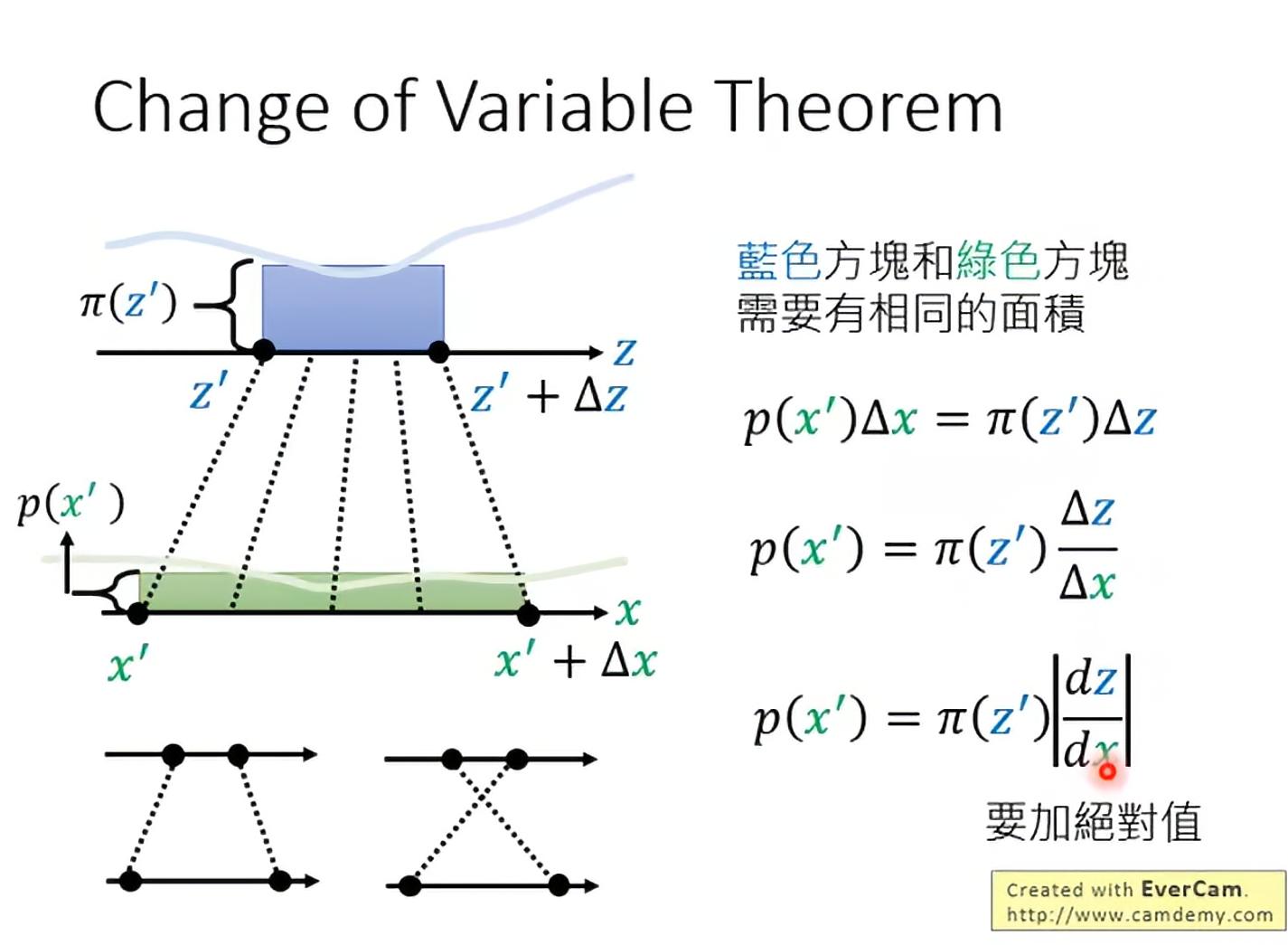
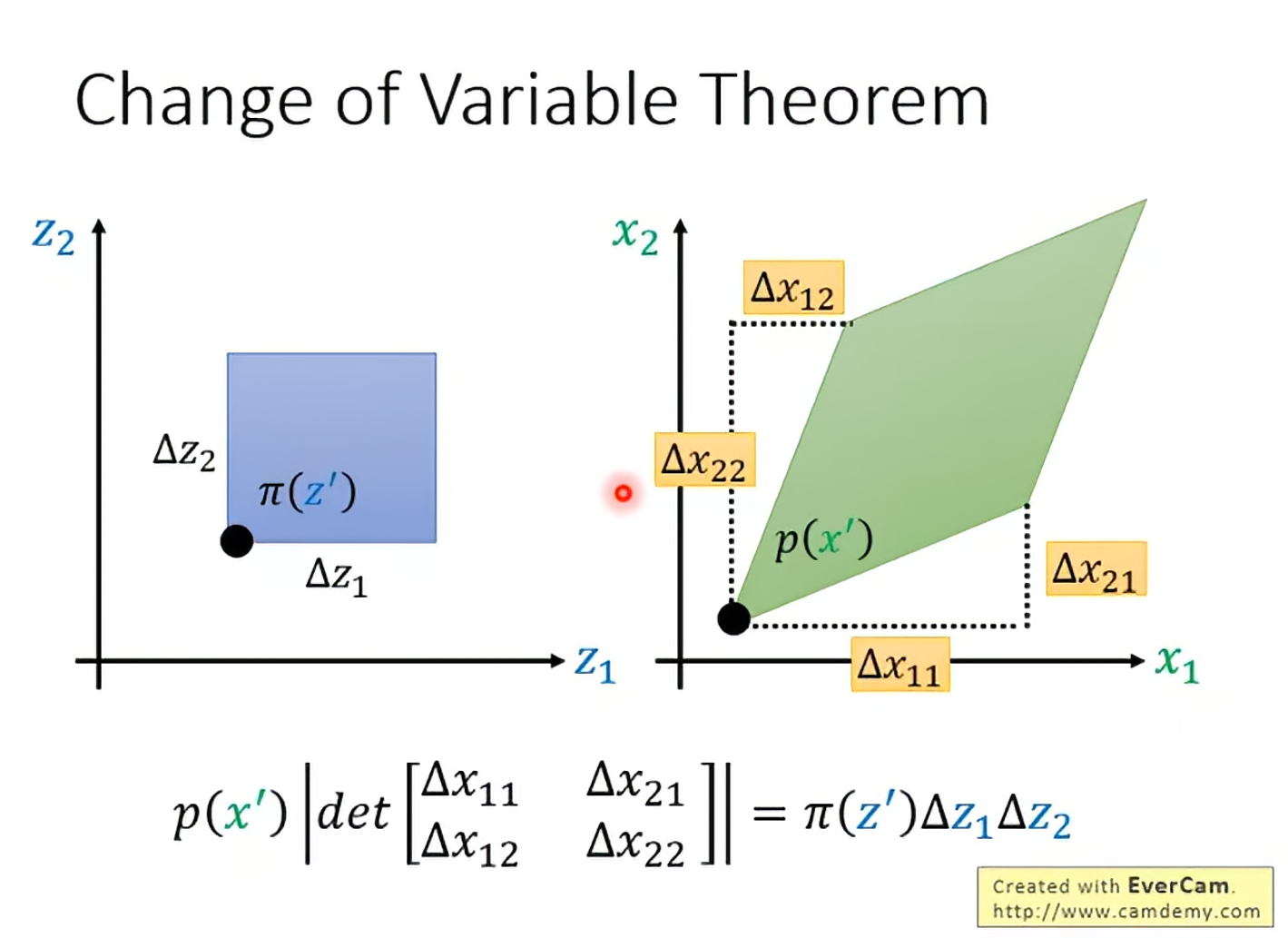

所以变换的系数就是一个jacobian matrix的行列式。
可以进入正题了:
我们本来要做的是最大化极大似然,重点是其中的
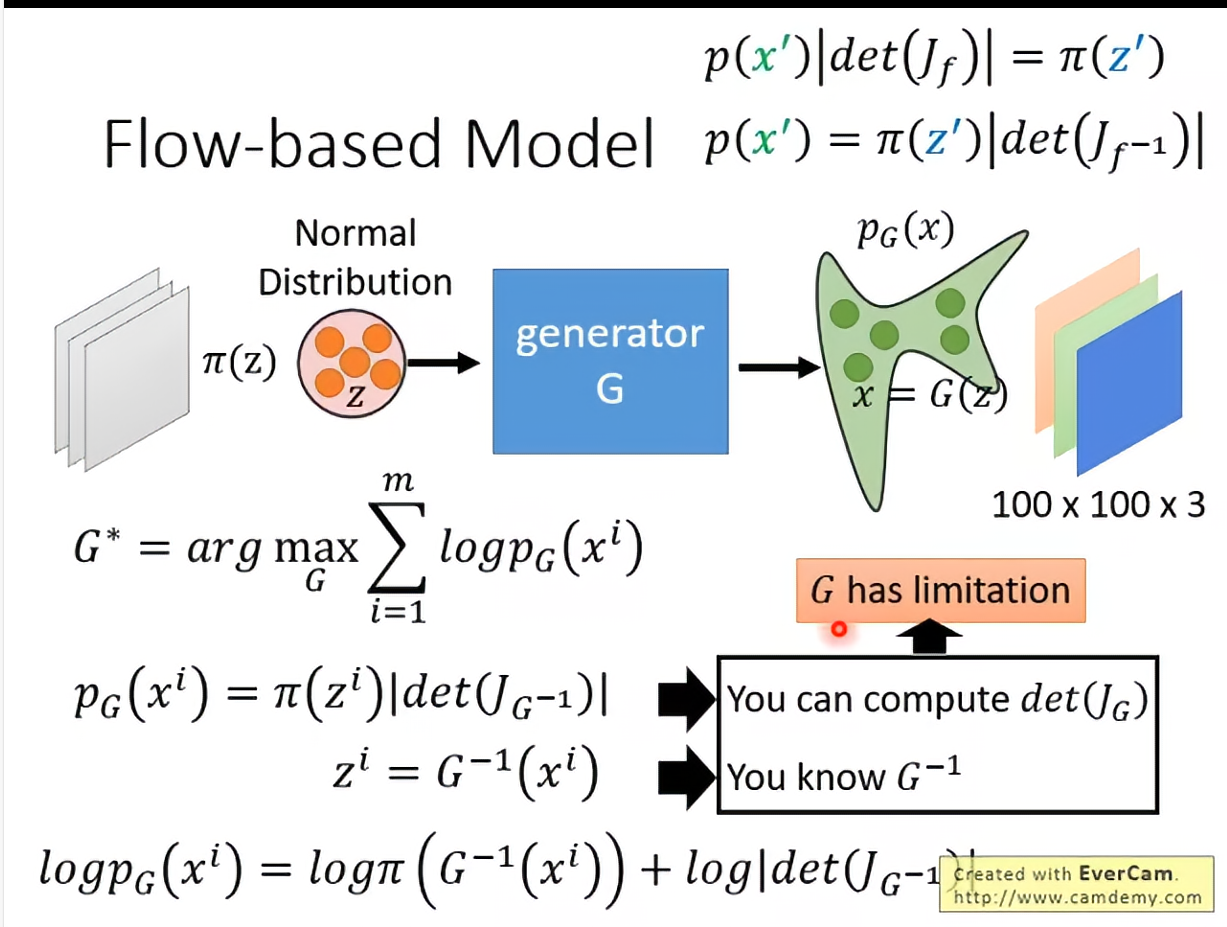
这样我们就把转化为了只与Generator有关的式子,而这个式子我们是用参数化的neural network来拟合的,也就是说可以直接做梯度下降。
虽然听上去很容易,实际上还是计算上的困难,计算也许没问题,但是可没有保证,因此我们需要特质化network架构,我们需要对G有限制,没有办法使用任意的G。(同时增添了限制,因为要求是inverable,所以Z的维度要和X一样,如果是图片的话维度会很大)
因为我们对G有限制,所以G的表示能力是有限的,所以可以像nn一样叠layers:
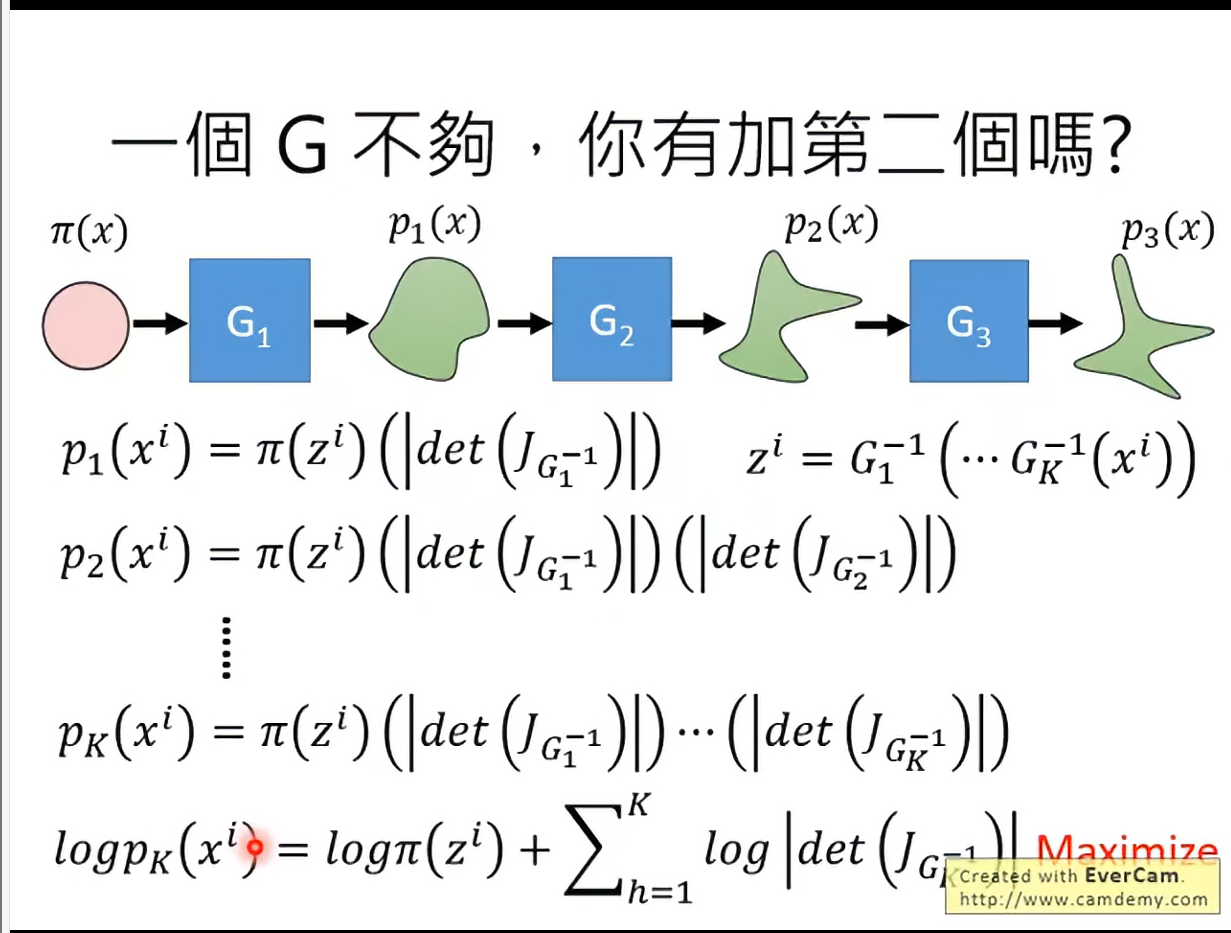
仔细看一下优化式子,只有,意味着我们只用训练,但是使用G去做生成。
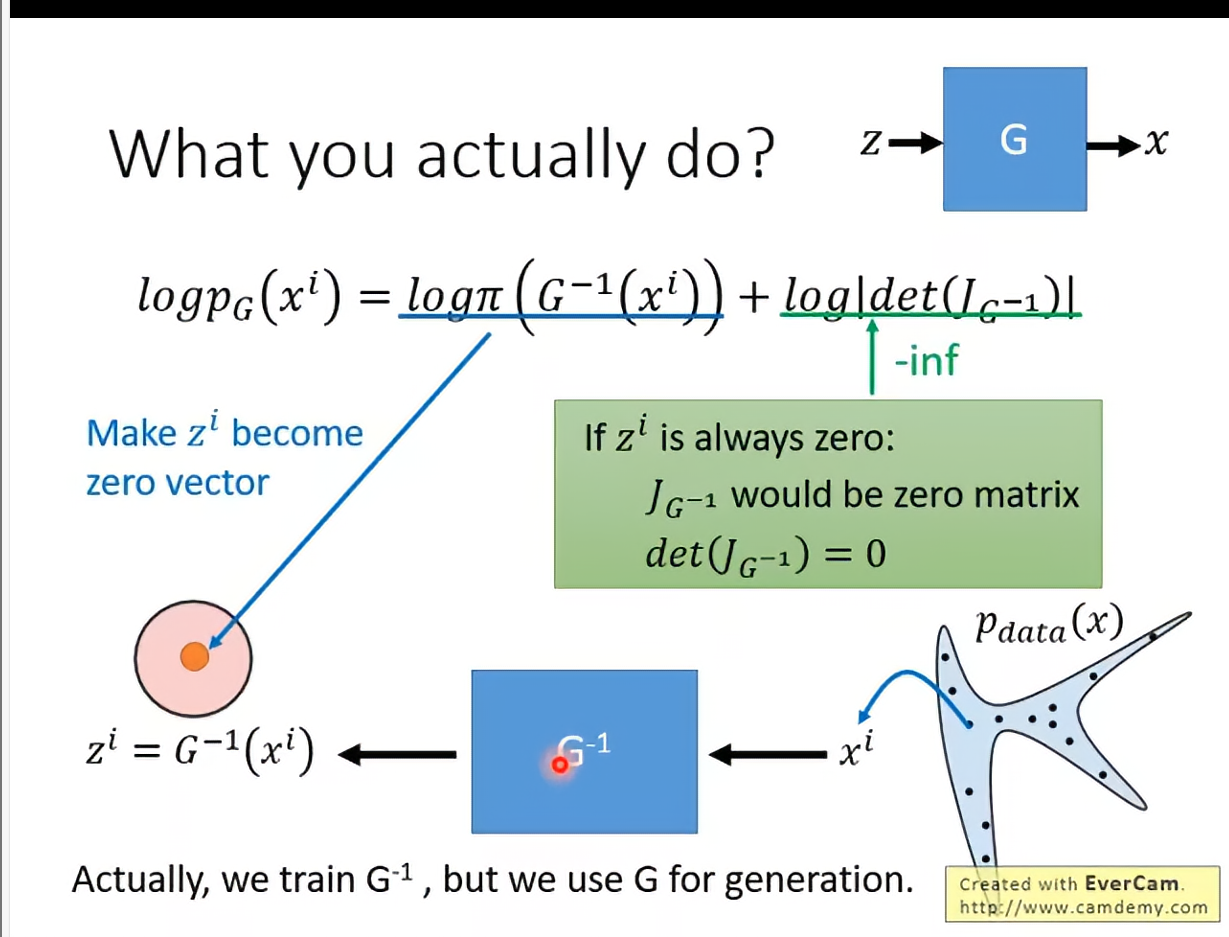
可以有一个直观的理解,我们实际在做的是train一个,每次从data里sample一个原始数据x,然后通过得到z,回想一下我们的z是默认正态分布的。
注意到第一个部分最大化:当然是越接近zero vector越好。
第二个部分:则限制了第一个部分,不能所有来啥你都映射到0,否则det会爆炸。
Coupling Layer
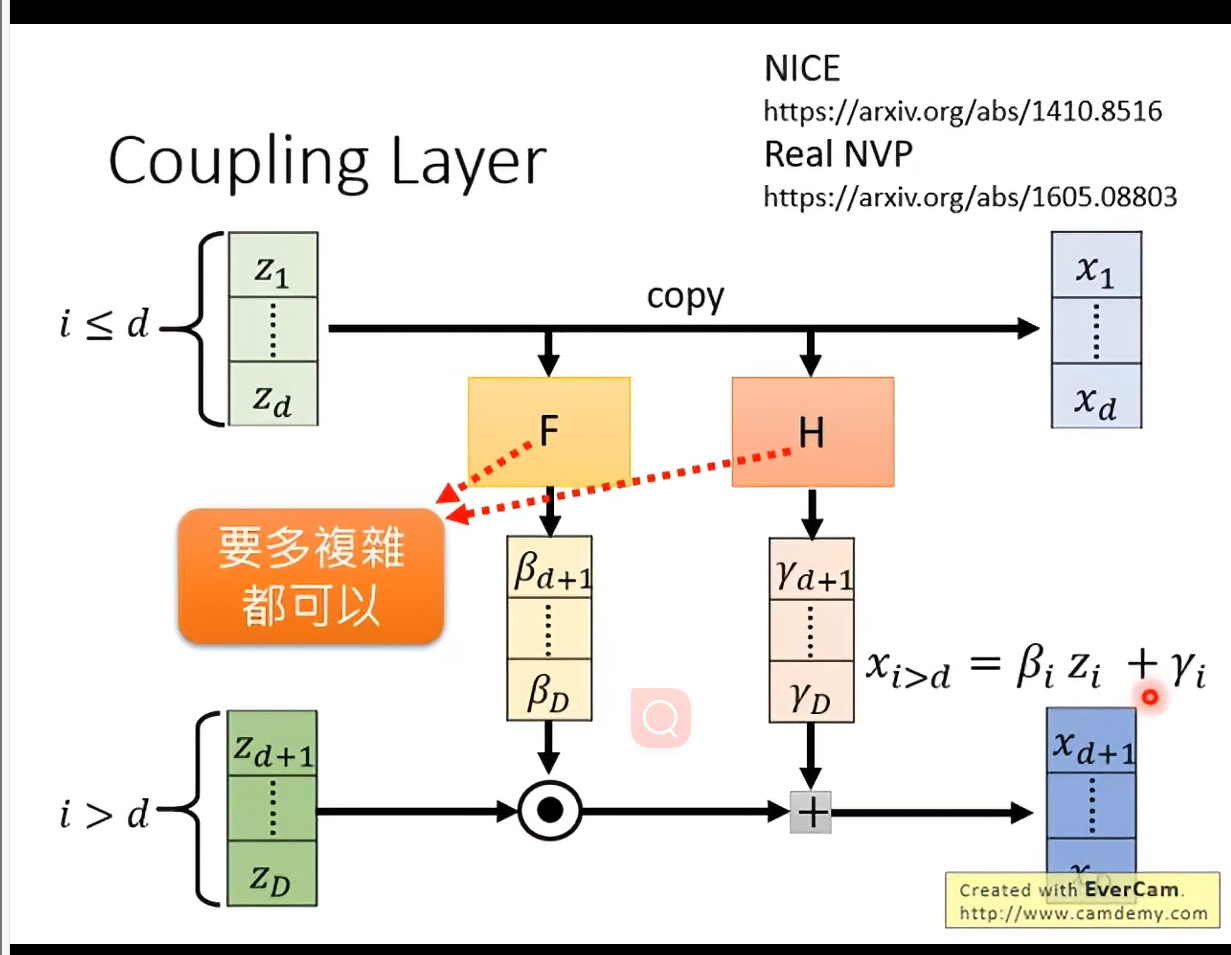
可以是arbitrary的function。
这样设计的好处,即是从的G inverse很好计算:
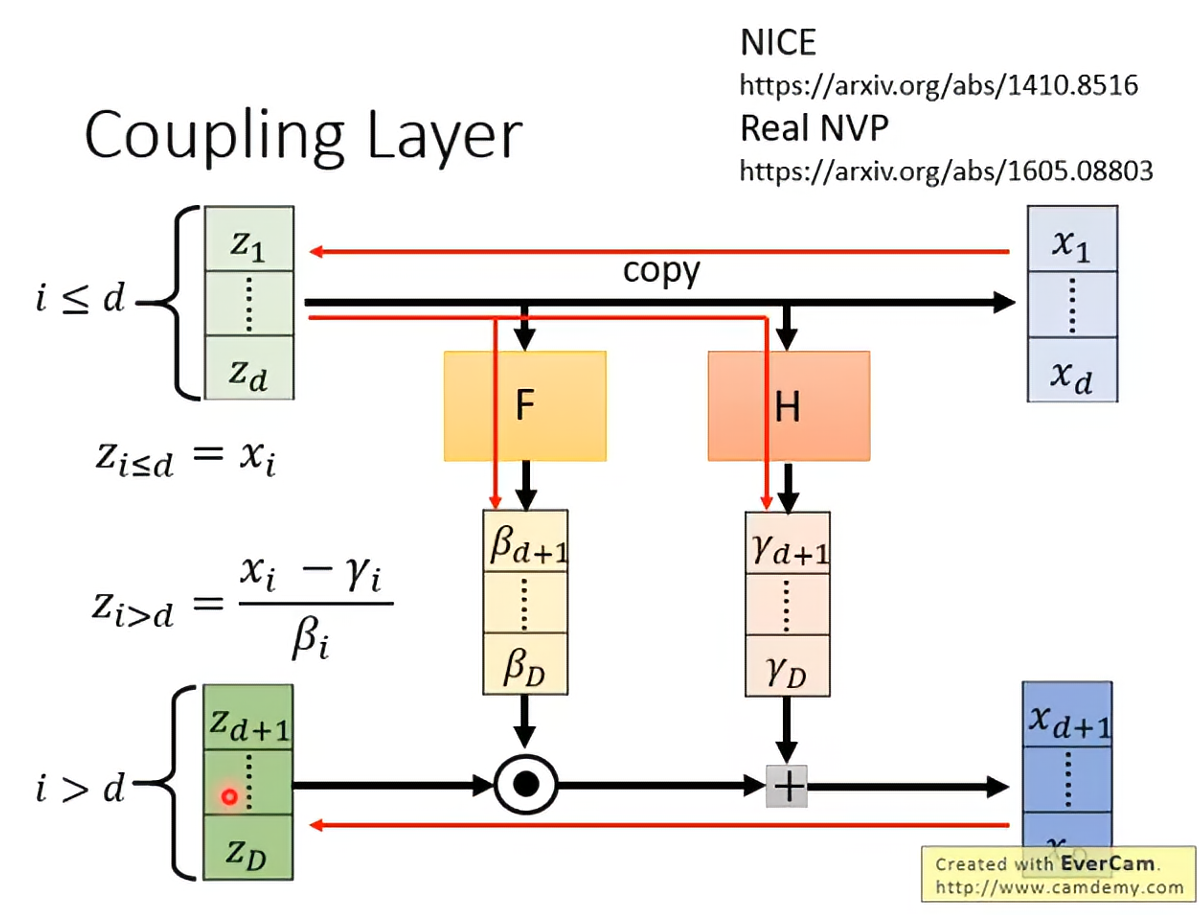
确实很妙,有种密码学的感觉hhh。
现在没有问题了,但是怎么算呢,如果维度大了,暴力算会很慢:
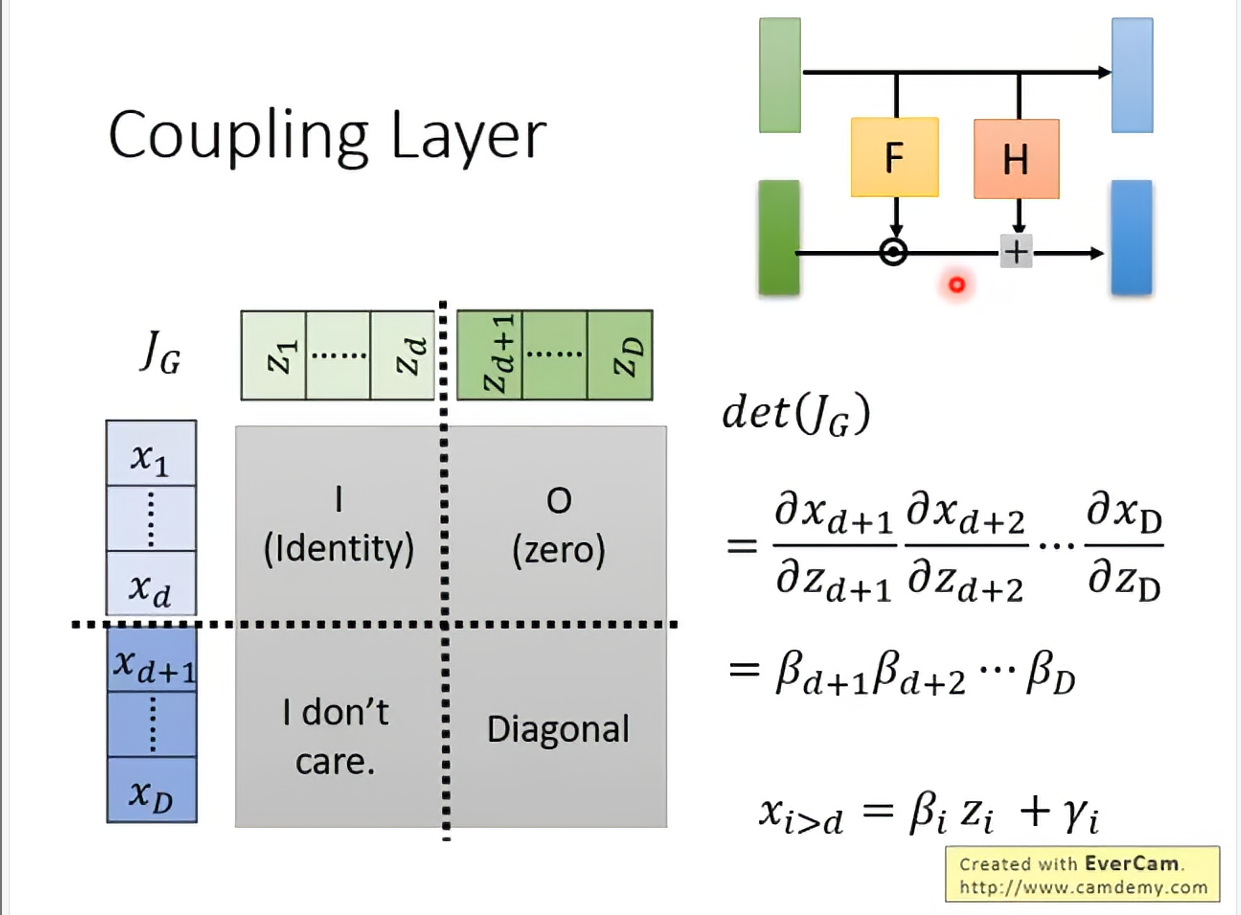
发下实际写出来就是,简直太好算了。
于是我们把这些coupling layer叠起来,就是一个flow-based model了。
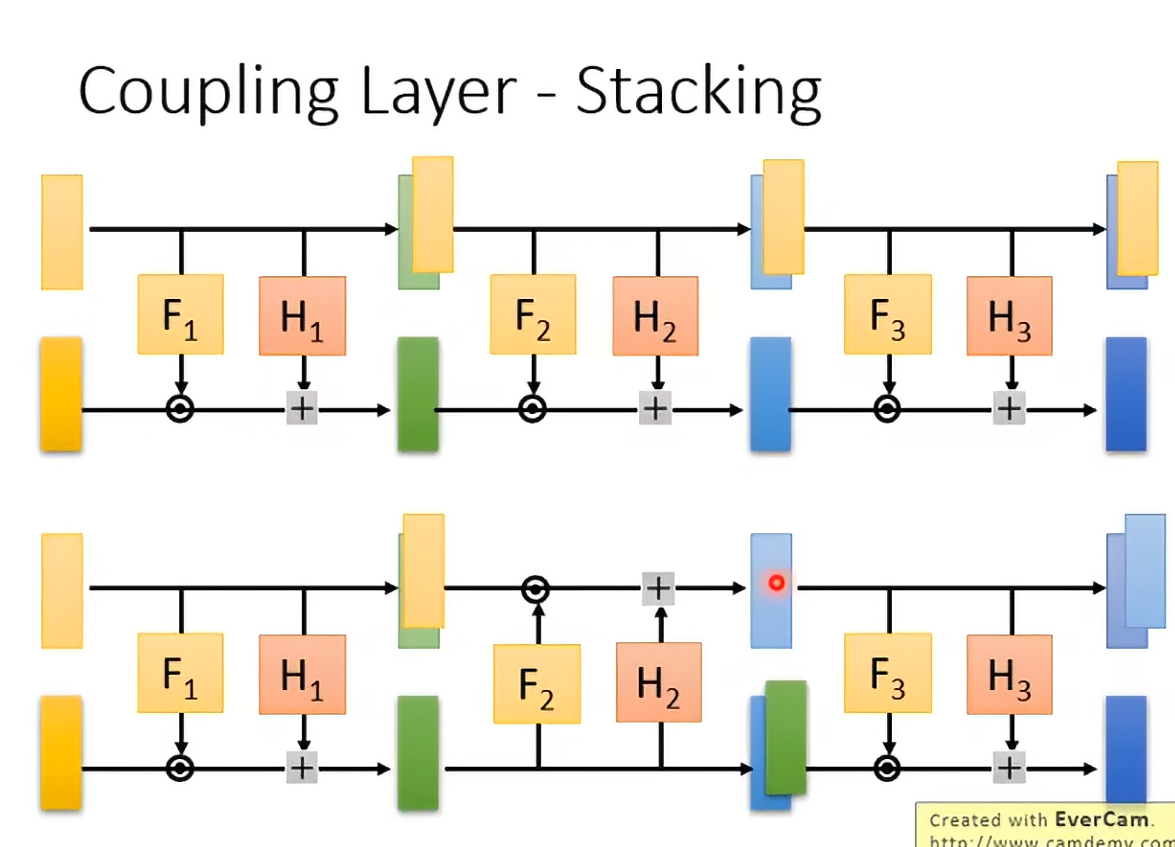
因为coupling layer有一段是直接复制的,所以我们很trick地不断调整复制段的位置。对于序列可以前半后半轮流,对于图像可以奇偶格子或者channel轮流。
GLOW
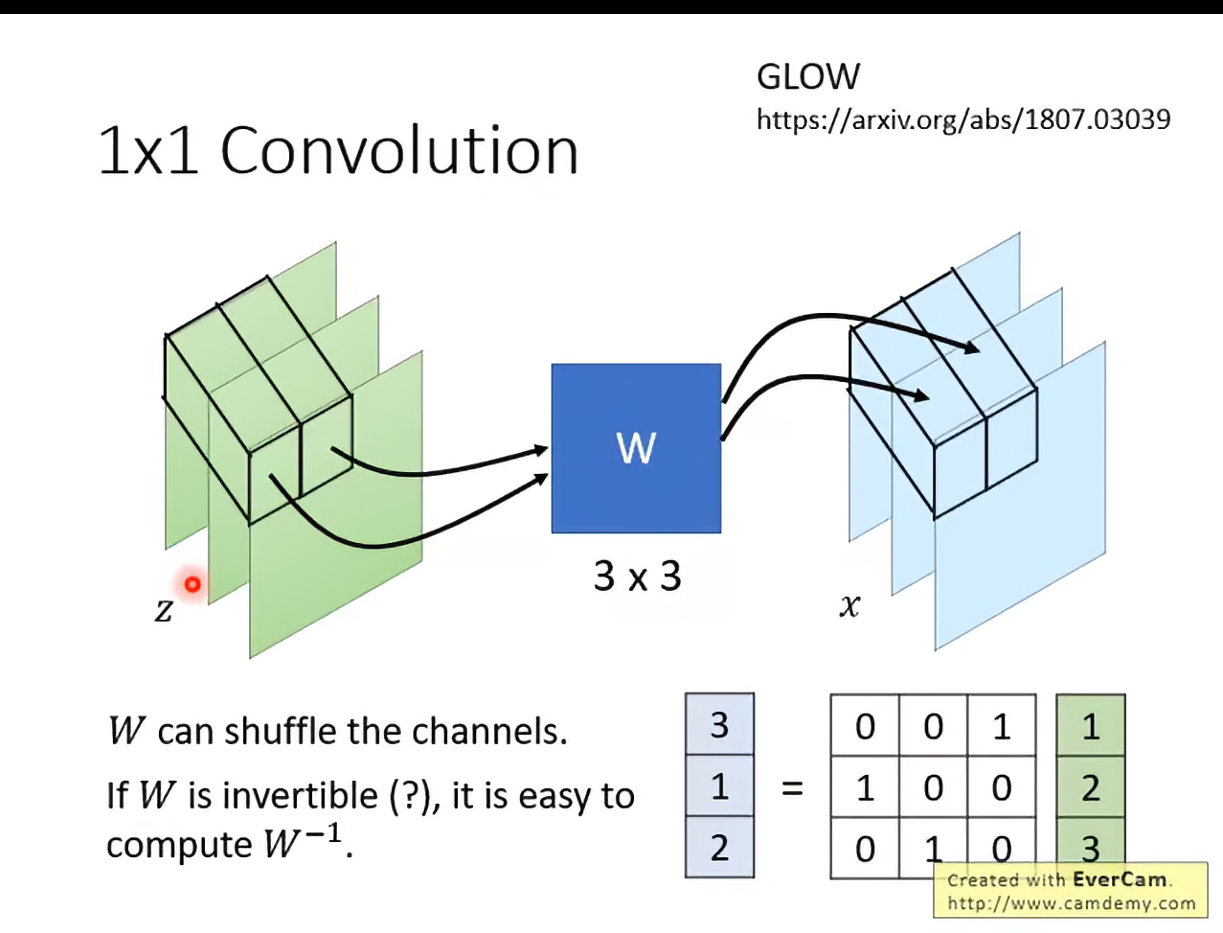
G的逆很好算↑
G的det也好算:
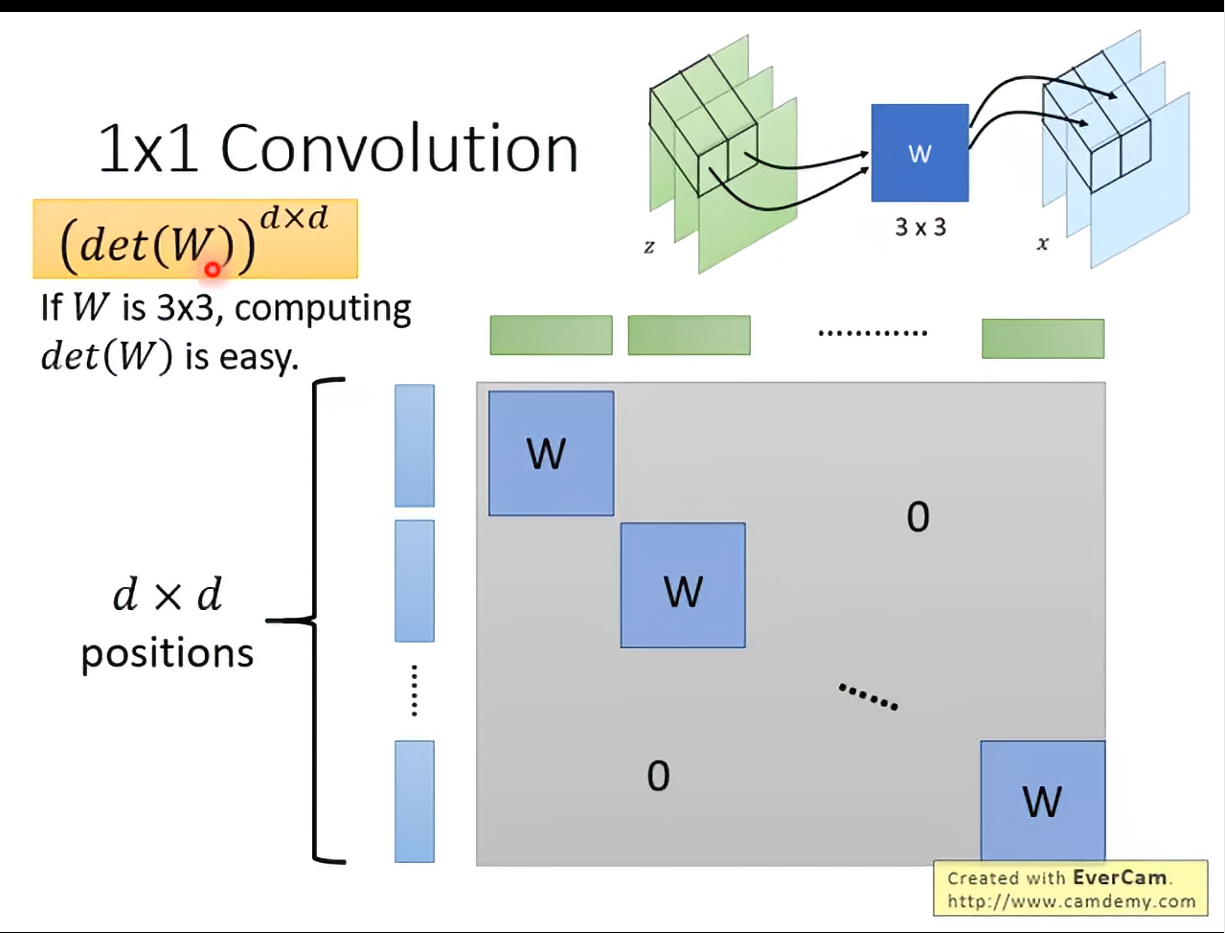
这样训练处encode()和decode()就可以做一些有趣的事情了。