网络流的基本概念

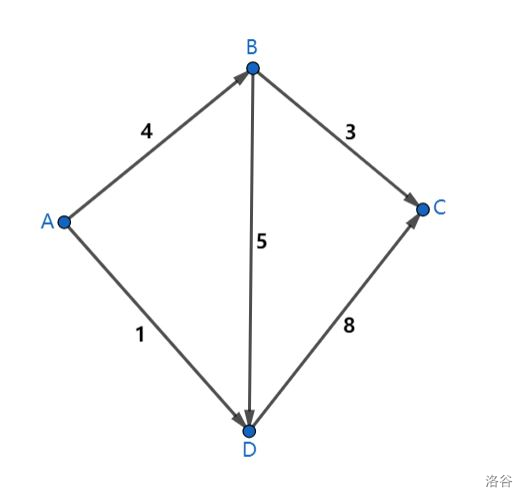
网络流问题都是建立在类似上图的有向图之上，有向图的边的权值代表容量。其中A代表源点，C代表汇点，一般考察的问题情景就是从A中流出流量，经过这些有向边，最终汇集到C中。像这样的具有源点和汇点，并且每条边的权值均为正数的有向图就被称作是容量网络，图中的这些边被称作是弧，弧的权值被称作弧的容量，它代表着能够通过这条弧的最大流量。而经过弧上的实际流量被称作弧的流量，所有这些弧的流量所组成的集合就是所谓的网络流。

直观上不难发现符合实际情况的网络流的特点，或者说是限制条件。首先每条弧上的流量不能超过其容量，还有对于除了源点和汇点以外的每个点来说，流入它的流量之和必须与从它流出的流量之和相等，即平衡条件。那么满足这两个条件的网络流就被称作是可行流，可行流的流量定义为从源点所流出的所有流量之和。在所有的可行流中，流量最大的那个被称作是最大流。

对于一串顶点序列(U,U1,U2,U3,…,V)(U,U1,U2,U3,…,V)，如果满足U是源点，V是汇点，并且序列中每相邻两个顶点之间均存在一条弧，那么就称这个顶点序列为一条链，注意这里并不要求这条弧的方向一定与有向图中的方向一致，在链中，弧被分为前向弧和后向弧，前向弧指在链中顶点的顺序与容量网络中弧的方向一致的弧，而后向弧则是方向不一致的弧。例如对于上图而言，(A,D,B,C)也是一条链，但是其中<A,D>、<B,C>是前向弧，<D,B>是后向弧。

有了链的定义就可以引出增广路的概念，对于可行流的一条链P，如果满足：

  1. P中所有的前向弧的流量小于容量
  2. P中所有的后向弧的流量均大于零

那么这条链P就被称作增广路。为什么要叫作增广路呢？因为增广路上的所有前向弧都是可以继续添加流量的（增加的流量不能超过每条前向弧的容量与流量之差），而反向弧上的流量都是可以继续减少的（减少的流量不能超过反向弧的流量），这两种措施都会使得这个可行流的流量变得更大。

割指的是一个弧的集合，将这个集合中的所有弧删除后原图的基图不再连通。割将原图中的所有顶点划分为两个部分，在网络流问题中，一般考虑的都是S-T割：即割将原图的顶点划分为两个部分S和T，源点∈S，汇点∈T。例如对于上图，将顶点划分为S=(A,B)、T=(C,D)S=(A,B)、T=(C,D)S=(A,B)、T=(C,D)的这样一个割就是S-T割。
对于割而言，也有流量和容量的概念。割的容量用C(S,T)表示，C(S,T)=∑c(u,v)(u∈S、v∈T、<u,v>∈E)(E代表容量网络所有弧的集合)，简单来说割的容量就是S中的所有点到T中所有点的前向弧的容量之和。例如对上图而言，割S=(A,B),T=(C,D)的容量为1+5+3=9。而对于割S=(A,D) T=(B,C)，它的容量为：4+8=12。在所有的割中，容量最小的割被称作最小割。
而割的流量指的是前向弧的流量之和减去后向弧的流量之和。因此割的流量小于等于割的容量，当且仅当割所划分的两个点集中不存在后向弧时取等。

最大流最小割定理及证明
网络流的最大流和最小割具有非常重要的实际意义，而这两者之间有着非常重要的关系：最大流的流量=最小割的容量，这就是最大流最小割定理，下面就来证明这个定理。

命题1：对于可行流的任意一个割，割的流量=可行流的流量

证明：采用归纳法，一开始只将T划分出去，此时任意可行流的流量是所有连T的流量和，此时满足。

考虑向T集合中新加入一点T1（T1的出边有向T集合的边，否则不可能加的进去），总的割加上T1的入边权值减去T1的出边权值，仍然不变。得证。

命题2：可行流的流量一定小于等于任意一个割的容量

证明：
由命题1显然可得：可行流的流量=割的流量≤割的容量

命题3：对于可行流G，设其流量为f，如下三个命题等价：

  1. 存在一个割使得割的容量c=f
  2. f是最大流的流量
  3. G中不存在任何增广路

1→21 \to 2 ：由命题2，任何一个可行流的流量都小于等于割的容量，即流量的上界是割的容量的最小值，而现在又存在一个割的容量c与f相等，故得证。

2→32 \to 3 : 证明逆否命题：若G中存在增广路，则f不是最大流的流量。由前面增广路的定义可知，增广路上的每条前向弧都可以继续增加流量，后向弧可以继续减少流量，这两种措施都会导致最终的流量变大，因此f不是最大流的流量。

3→13 \to 1 G中不存在任何增广路，意味着由源点到汇点的任何一条链中一定存在饱和前向弧（流量=容量）或者零流后向弧（流量=0）。这说明如果只通过非饱和前向弧和非零流后向弧绝对不可能从源点运动到汇点，那么取割(S,T)，其中S为源点能够通过非饱和前向弧和非零流后向弧到达的所有顶点构成的集合，T为剩下的点构成的集合，S中的所有点都不能通过非饱和前向弧和非零流后向弧到达T，也就是说S与T之间的弧一定都是饱和前向弧或者零流后向弧，

有

割的流量 = 前向弧流量 - 后向弧流量 = 前向弧流量 - 0 = 前向弧流量 = 前向弧容量=割的容量。

因此一定存在一个割，满足割的流量 = 割的容量。

由此就证明了这三个命题等价，同时论证了最大流最小割定理。

由此就不难想到求解最大流的算法，可以在可行流G中不断地寻找增广路，如果不存在增广路，此时可行流就是最大流；如果存在增广路，就在增广路上作修正。这样不断地迭代下去，直到不存在增广路为止。

前面啰嗦了这么多废话，现在来看看更废话的网络流实现。

最大流

我们将每条边连一条反边，使的我们可以反悔（只是在效果上可以反悔，实际效果是中间的反悔边走了两次，相当于在其两头将两条路径交换了一下。）

不断地寻找增广路，如果不存在增广路，此时可行流就是最大流；如果存在增广路，就在增广路上作修正。这样不断地迭代下去，直到不存在增广路为止。

一点优化：

  1. 当前弧优化，因为每一次dfs从一个点走向另一个点时，如果已经把其流量榨干了，可以跳过这些点。

  2. 若已经把流用完了，可以break了。

  3. dfs时走完一个点，若走不通（sum=0），那么此点在本次dfs中不用再考虑。

code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=205,M=10005;
inline int getint(){
	int summ=0,f=1;char ch;
	for(ch=getchar();!isdigit(ch)&&ch!='-';ch=getchar());
	if(ch=='-')f=-1,ch=getchar();
	for(;isdigit(ch);ch=getchar()) summ=(summ<<3)+(summ<<1)+ch-48;
	return summ*f;
}
int head[N],nex[M],go[M],w[M],dep[N],tot=1,S,T,cur[N],n,m;
inline void add(int u,int v,int val){
	nex[++tot]=head[u];head[u]=tot;go[tot]=v;w[tot]=val;
}
inline bool bfs(){
	queue <int> q;q.push(S);
	memset(dep,-1,sizeof(dep));dep[S]=1;
	for(int i=1;i<=n;i++) cur[i]=head[i];
	while(!q.empty()){
		int u=q.front();q.pop();
		for(int i=head[u];i;i=nex[i]){
			int v=go[i];
			if(dep[v]==-1&&w[i]){
				dep[v]=dep[u]+1;q.push(v);
			}
		}
	}
	return dep[T]!=-1;
}
int dfs(int u,int lim){
	if(u==T||!lim) return lim;
	int res=0;
	for(int i=cur[u];i;i=nex[i]){
		cur[u]=i;
		int v=go[i];
		if(dep[v]==dep[u]+1&&w[i]){
			int sum=dfs(v,min(lim-res,w[i]));
			if(sum){
				w[i]-=sum;w[i^1]+=sum;res+=sum;
			}
		}
		if(lim==res) break;
	}
	return res;
}
signed main(){
	cin>>n>>m>>S>>T;
	for(int i=1,u,v,val;i<=m;i++){
		u=getint();v=getint();val=getint();
		add(u,v,val);add(v,u,0);
	}
	int ans=0;
	while(bfs()) ans+=dfs(S,1e18);
	cout<<ans<<endl;
	return 0;
}

费用流

我们每次要找最小代价的增广路，用spfa解决。

最后回溯最短路径改流即可。

code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include<bits/stdc++.h>
using namespace std;
inline int getint(){
	int summ=0,f=1;char ch;
	for(ch=getchar();!isdigit(ch)&&ch!='-';ch=getchar());
	if(ch=='-')f=-1,ch=getchar();
	for(;isdigit(ch);ch=getchar()) summ=(summ<<3)+(summ<<1)+ch-48;
	return summ*f;
}
const int N=5005,M=100005;
int dep[N],tot=1,head[N],nex[M],go[M],vis[N],w[M],d[M],dis[N],n,m,S,T,fa[N],las[N],flow[N];
inline void add(int u,int v,int fl,int val){
	nex[++tot]=head[u];head[u]=tot;go[tot]=v;w[tot]=fl;d[tot]=val;
}
inline bool spfa(){
	queue <int> q;q.push(S);
	memset(vis,0,sizeof(vis));
	memset(dis,0x7f,sizeof(dis));
	memset(flow,0x7f,sizeof(flow));
	vis[S]=1;dis[S]=0;
	while(!q.empty()){
		int u=q.front();q.pop();vis[u]=0;
		for(int i=head[u];i;i=nex[i]){
			int v=go[i];
			if(w[i]&&dis[v]>dis[u]+d[i]){
				dis[v]=dis[u]+d[i];flow[v]=min(flow[u],w[i]);
				fa[v]=u;las[v]=i;
				if(!vis[v]){
					vis[v]=1;q.push(v);
				}
			}
		}
	}
	return dis[T]!=dis[0];
}
signed main(){
	cin>>n>>m>>S>>T;
	for(int i=1,u,v,fl,val;i<=m;i++){
		u=getint();v=getint();fl=getint();val=getint();
		add(u,v,fl,val);add(v,u,0,-val);
	}
	int maxflow=0,mincost=0;
	while(spfa()){
		maxflow+=flow[T];mincost+=flow[T]*dis[T];
		int now=T;
		while(now!=S){
			w[las[now]]-=flow[T];
			w[las[now]^1]+=flow[T];
			now=fa[now];
		}
	}
	cout<<maxflow<<" "<<mincost;
	return 0;
}

最小割

板子就是最大流。

例题

接下来是菜鸡的例题大赏。

（链接是我的题解传送门）

这是个好题，值得分析。

首先我考虑的是一个点连其横边和竖边，跑最大流最小费用，但是这有个致命的问题，我们没法控制选了一个点后要流向横边or竖边or横竖都流。（但是竟然过了垃圾数据）

分析我们失败原因，我们没法控制一个点的选择，于是我们转变思路，选择一个点意味着其横纵向边+1，那么不难想到加入一个点，只连其横向点到纵向点流量为1，只要保证入边是横向边且大于限制，出边是横向边且大于限制，最小流即使答案。

于是上下界最小流可以搞定。

然而我们都知道上下界网络流难写又难调，思考有没有简单的做法。

补集转化，那么条件变成第ii行不放士兵的位置不超过n−L[i]n-L[i]，第jj列不放士兵的位置不超过m−C[i]m-C[i]，求最多不放多少个士兵.

我们发现，这成了最大流板题。

至此问题得以快速的解决且方便的实现。

Trick

  • 出边回流问题

因为网络流源点可以无限流出，故只要发现一条从源点出去的增广路，那么肯定存在一种最优流方案包含这条增广路。（大不了多浪费点源点的出量）

于是在解决要求按照字典序输出方案的网络流费用流问题中，（前提：只有出边有费用）可以按照出边按照费用为第一关键字，字典序为第二关键字排序，这样安好排列顺序用匈牙利跑出边的增广路，这样保证了费用最小同时满足构造的字典序最小。

这启示我们要从网络流图形的特殊性思考。

例题

在建网络流时，可以发现只有起点出边有费用，更惊喜的是网络流出边不会回流，也就是说我们可以按照最小生成树的方法先给每条出边以费用为第一关键字，字典序为第二关键字排序，再用匈牙利算法判断是否可以增广，就完美解决了字典序问题。

code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
#include<bits/stdc++.h>
using namespace std;
#define int long long
int getint(){
	int summ=0,f=1;
	char ch;
	for(ch=getchar();!isdigit(ch)&&ch!='-';ch=getchar());
	if(ch=='-'){
		f=-1;
		ch=getchar();
	}
	for(;isdigit(ch);ch=getchar())
	summ=(summ<<3)+(summ<<1)+ch-48;
	return summ*f;
}
struct node{
	int x,y,pw;
}a[1000];
struct node1{
	int x,y,lim,pri,mx,fin,op,id;
	bool operator < (const node1 &yy) const{
		if(pri==yy.pri) return id<yy.id;
		return pri<yy.pri;
	}
}b[1000];
int n,m,now;
const int M=300000;
int bi=1,S,nn,T,tot,mincost,maxflow,pa[M],from[M],nex[M<<1],head[M],go[M<<1],w[M<<1],d[M<<1],fl[M],dis[M],pre[M],vis[M],last[M]; 
inline int getdis(int x,int y){
	return (b[x].x-a[y].x)*(b[x].x-a[y].x)+(b[x].y-a[y].y)*(b[x].y-a[y].y);
}
inline void add(int u,int v){
	nex[++tot]=head[u];head[u]=tot;go[tot]=v;
}
int ma=0,re[M],ans;
bool dfs(int x){
	for(int i=head[x];i;i=nex[i]){
		int v=go[i];if(vis[v]==now) continue;
		vis[v]=now;
		if(!from[v]||dfs(from[v])){
			from[v]=x;return true;
		}
	}
	return false;
}
signed main(){
	//freopen("dream.in","r",stdin);
	//freopen("dream.out","w",stdout);
	int TT;cin>>TT;
	while(TT--){
		memset(head,0,sizeof(head));
		memset(from,0,sizeof(from));
		memset(pa,0,sizeof(pa));
		memset(vis,0,sizeof(vis));
		tot=1;S=0;mincost=maxflow=0;
		cin>>n>>m;T=n+m+1;nn=0;ma=0,ans=0;
		for(int i=1;i<=n;i++){
			a[i].x=getint();a[i].y=getint();a[i].pw=getint();
		}
		for(int i=1;i<=m;i++){
			b[i].x=getint();b[i].y=getint();b[i].lim=getint();b[i].pri=getint();b[i].mx=getint();b[i].fin=getint();
			if(b[i].fin) ans+=b[i].pri,b[i].pri=-b[i].pri;b[i].id=i;
		}
		sort(b+1,b+m+1);
		for(int i=1;i<=m;i++)
	      for(int j=1;j<=n;j++){
	  	    if(getdis(i,j)<=b[i].mx*b[i].mx&&b[i].lim>=a[j].pw){
	  	    	add(i,j);
	  	    }
	  	}
	  	int sum=0;
	  	for(now=1;now<=m&&sum<=n;now++){
	  		if(dfs(now)) ans+=b[now].pri,sum++,pa[b[now].id]=1;
	  	}
	  	if(sum<n) cout<<-1<<"\n";
	  	else{
	  		cout<<ans<<"\n";
	  		for(int i=1;i<=m;i++) if(pa[i]) cout<<i<<" ";cout<<"\n";
	  	}
	}
	return 0;
}

  • 最小割树

作用：快速求解两点间最小割

流程：

  1. 先建立一个无向图，然后再把这个图的整体看做一个集合，然后任意选择两个点在原图上跑一趟最小割。

  2. 然后，我们再对每个集合进行这样的操作（注意，最小割要在原图上跑），再分下去，直到集合内只剩一个节点为止。

  3. 最后，我们可以得到一棵最小割树。

这里要注意，跑最小割（最大流）要在原图上跑！！！

性质：

这棵树中任意两点的最小割等于原图上任意两点的最小割

一点证明：

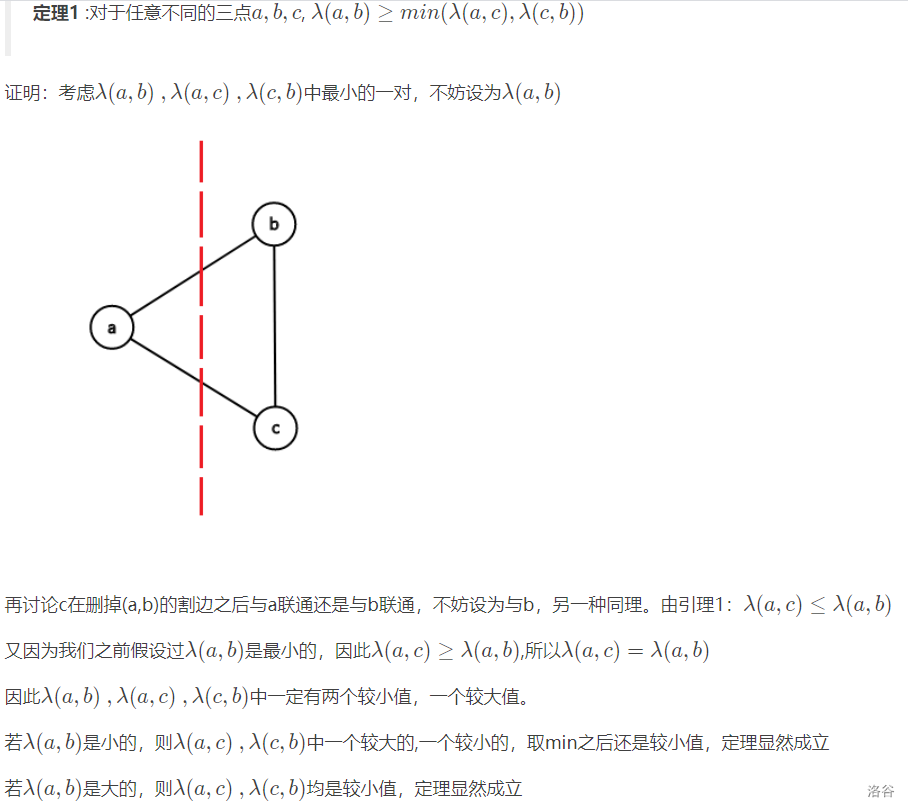
理解不了的话，这结论其实既直观又好背。

分治建树过程：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int node[maxv];//node[i]里面存储点的编号
int tmp1[maxv],tmp2[maxv];
void build(int l,int r){
        if(l==r) return;
        int s=node[l],t=node[l+1];//任选两个点
        int cut=network_flow::dinic(s,t);
        add_edge(s,t,cut);
        int cnt1=0,cnt2=0;
        for(int i=l;i<=r;i++){
            if(network_flow::deep[node[i]]) tmp1[++cnt1]=node[i];
            else tmp2[++cnt2]=node[i];
            //考虑dinic算法中的最后一次bfs,因为现在残量网络上s到达不了t,所以bfs访问到的点就是s所在的点集，它们的deep不0
        }
        for(int i=l;i<=l+cnt1-1;i++) node[i]=tmp1[i-l+1];
        for(int i=l+cnt1;i<=r;i++) node[i]=tmp2[i-cnt1-l+1];
        build(l,l+cnt1-1);
        build(l+cnt1,r);
    }

然后就可以切掉这道cqoi 最小割树板题了