贝叶斯网络与MCMC近似

贝叶斯网络的结构

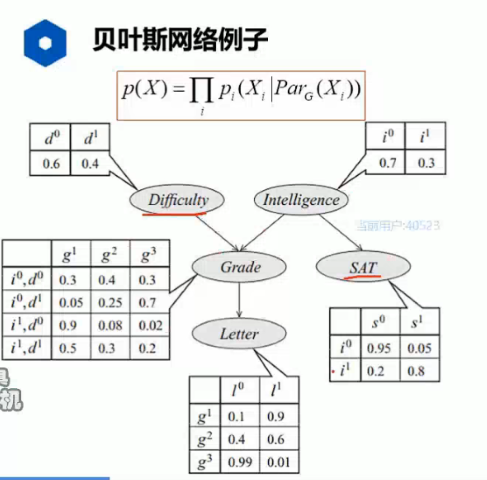
计算联合分布：

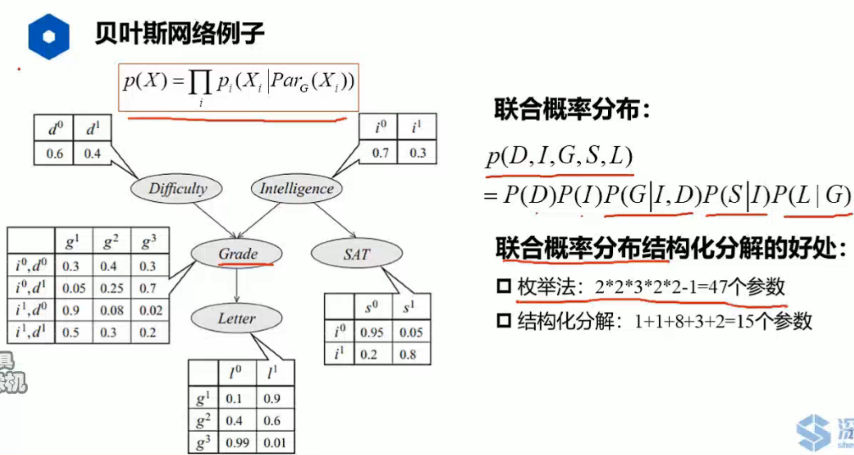
有利于减少参数量。(因为计算中每个节点只与父节点相关)

贝叶斯网络的建立

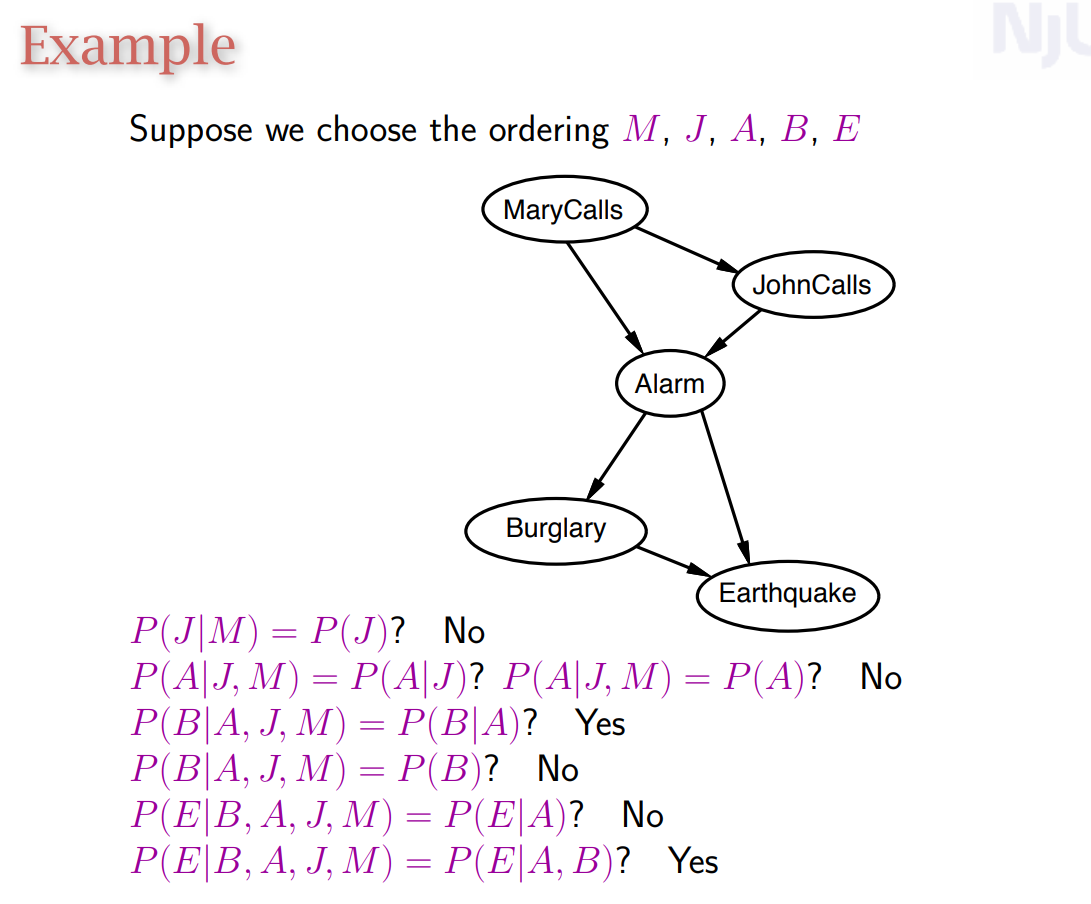
按照上述方式至少可以建DAG，但是想让图最自然同时边最少，需要按照逻辑拓扑序建图。

反过来也说明贝叶斯网络对图如何建立的不敏感。

贝叶斯网络的性质

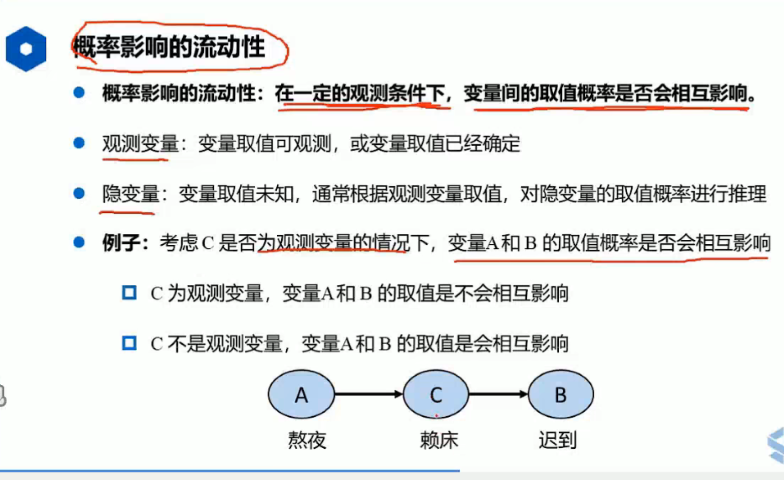
流动性特点：

X,Y为节点，Z为观测变量的集合

有效迹

更具流动性的特点，可以引入d-分离的概念。

• 定理1：父节点已知时，该节点与其非后代节点条件独立。（根据有效迹可以判断）

• 定理2：Markov blanket：Each node is conditionally independent of all others given its Markov blanket: parents + children + children’s parents

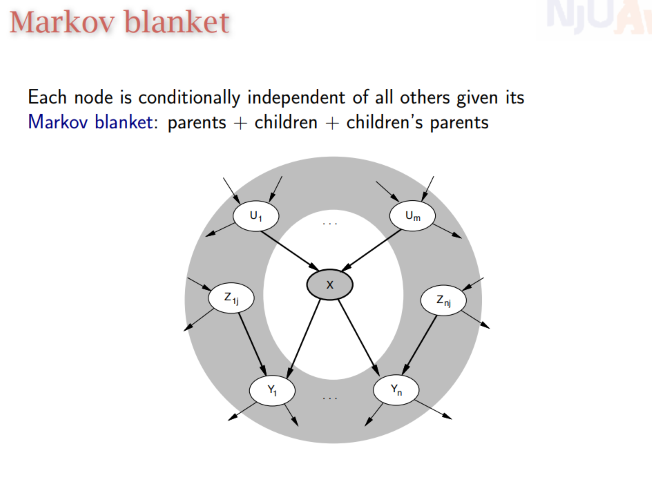
计算条件独立时可化简

• 计算条件概率时，可以通过条件独立大大化简原式子。（每个部分的概率只依赖于不多的与之相关的节 点）。

特别需要注意下：

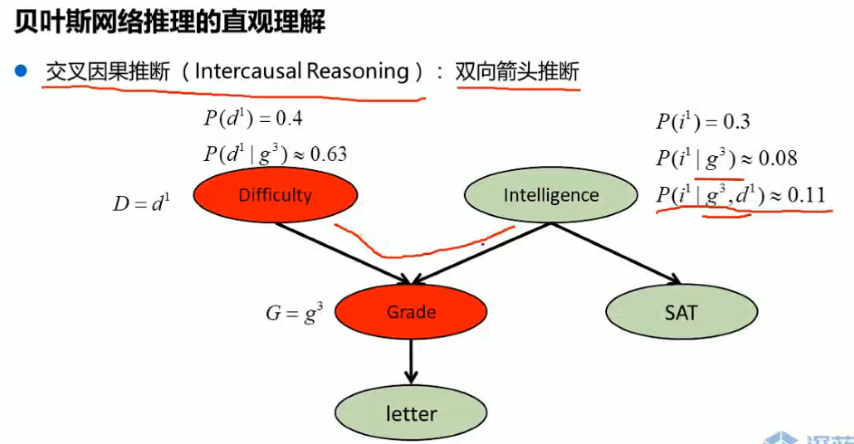
在给定G时，D与I是有流动性的，此时D与I是不独立的。
反之，若不给定G，D与I之间没有有效迹，是独立的。

虽然已经简化了很多，但是具体推理的时候还是一个np问题。

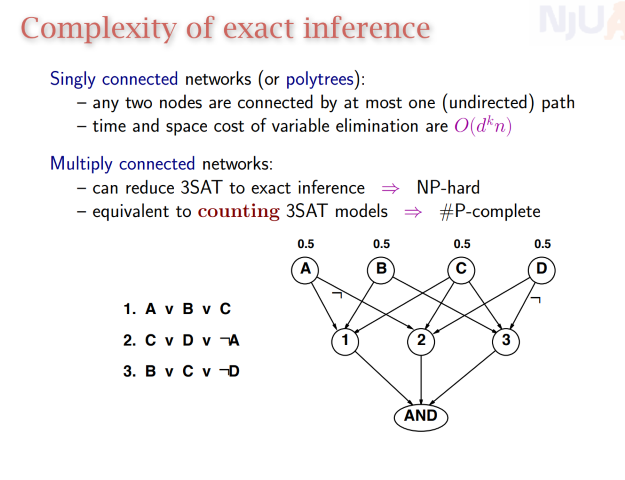
所以我们需要一个可以快速计算的方法。

Approximate Inference

Sampling from an empty network

暴力抽签法

Rejection Sample

对于不满足条件conditon就直接不抽，这样省的时间在所有抽样里找到满足条件。

但，其实这样的方法与random方法效果相同时，需要的抽数是一样的。

Likelyhood weighting

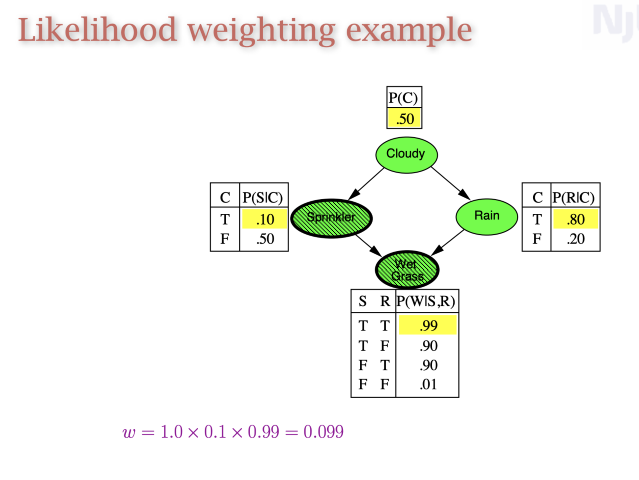
两者细节&&关系：

MCMC

• MCMC与贝叶斯推断简介：从入门到放弃

这篇文章总结的很好。

简要说一下我的理解：

$\pi P=\pi$

$\pi$是一个概率分布，P是一个转移矩阵，$\pi P$是一个新的概率分布。

如果一开始按照概率密度取样，取样的结果可以用$\pi$来表示。

那么按照当前的取样结果，作为条件变量，再次取样，取样的结果可以用$\pi P$来表示。

也就是说我们取得每一个样都是满足$\pi$的，于是通过重复多次的这样取样，我们可以得到一个满足$\pi$的样本集。达到目的。

---

但是这样有一个问题，这个$P$转移矩阵不太好构造（要求对于$\pi$平稳分布）

如果我们能基于简单随机取样就可以间接实现这个转移矩阵的构造就好了。

引入接受参数，配合对称的简单概率密度分布函数（均匀分布，正态分布），就可以实现这个转移矩阵的间接构造。

---

Approximate inference using MCMC

最常见的MH采样：

接下来是吉普斯取样法：

吉普斯采样因为可以和贝叶斯图性质相结合，所以在贝叶斯图采样中占主流。

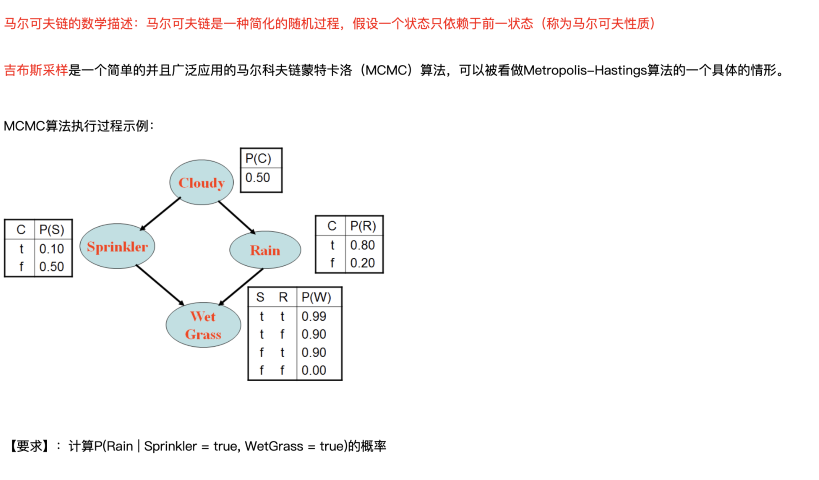
• 吉普斯采样法特点

吉普斯采样法正确性说明

• 证明法一：

• 证明法二：

同时，非常重要的一点，因为我们引入贝叶斯网络的原因，所以我们可以利用贝叶斯网络的结构来加速吉普斯采样法。

对于$p(x_i|{x_{-i}})$只用考虑$x_i$的马尔科夫团即可。（根据流动性原理，一旦马尔科夫团确定，其他节点都是条件独立不用再去计算。）

蒙特卡洛马尔可夫链估计法正确性说明

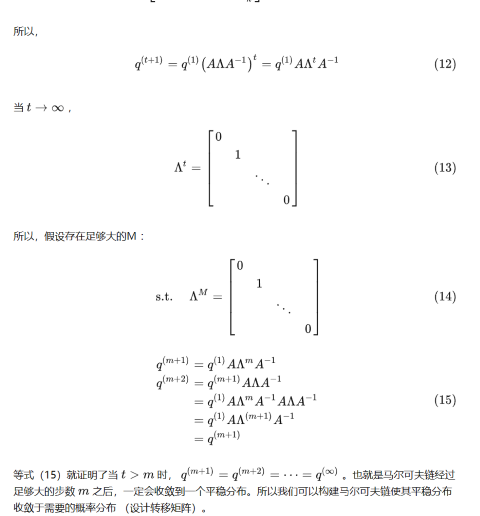
MCMC采样过程中的一些问题

• 无法判断是否已经收敛。
• 燃烧期过⻓，这就是有高维所造成的，维度和维度之间的相关性太强了，可能无法采样到某些维度。
• 样本之间一定是有相关性的，如果每个时刻都取一个点，那么每个样本一定和前一个相关，这可以通过间隔一段时间采样。