DS作业汇报 Fibonacci堆

detect0530@gmail.com

探究Fibonacci堆对dijkstra算法的优化效果

复杂度分析，与常见堆结构的理论横向对比
实现Fibonacci堆
验证Fibonacci堆的正确性
- 利用qt实现可视化效果，方便调试
- 设定check函数，自动检测堆性质以及双向链表的正确性
- 与其他堆以及stl提供的priority_queue进行对拍比较
将正确性得到保证的Fibonacci堆应用到dijkstra算法中，并在随机&高压数据集上进行测试，并记录实验结构
分析实验结果，得出结论

操作 `\` 数据结构	配对堆	二叉堆	左偏树	二项堆	斐波那契堆
插入（insert）	$O(1)$	$O(\log n)$	$O(\log n)$	$O(\log n)$	$O(1)$
查询最小值（find-min）	$O(1)$	$O(1)$	$O(1)$	$O(1)$	$O(1)$
删除最小值（delete-min）	$O(\log n)$	$O(\log n)$	$O(\log n)$	$O(\log n)$	$O(\log n)$
合并 (merge)	$O(1)$	$O(n)$	$O(\log n)$	$O(\log n)$	$O(1)$
减小一个元素的值 (decrease-key)	$o(\log n)$ （下界 $\Omega(\log \log n)$ ，上界 $O(2^{2\sqrt{\log \log n}})$ ）	$O(\log n)$	$O(\log n)$	$O(\log n)$	$O(1)$
是否支持可持久化	$\times$	$\checkmark$	$\checkmark$	$\checkmark$	$\times$

在dijkstra算法中，我们需要频繁的进行insert操作，而Fibonacci堆在insert操作上有着极大的优势，因此我们期望Fibonacci堆在dijkstra算法中有着更好的表现。

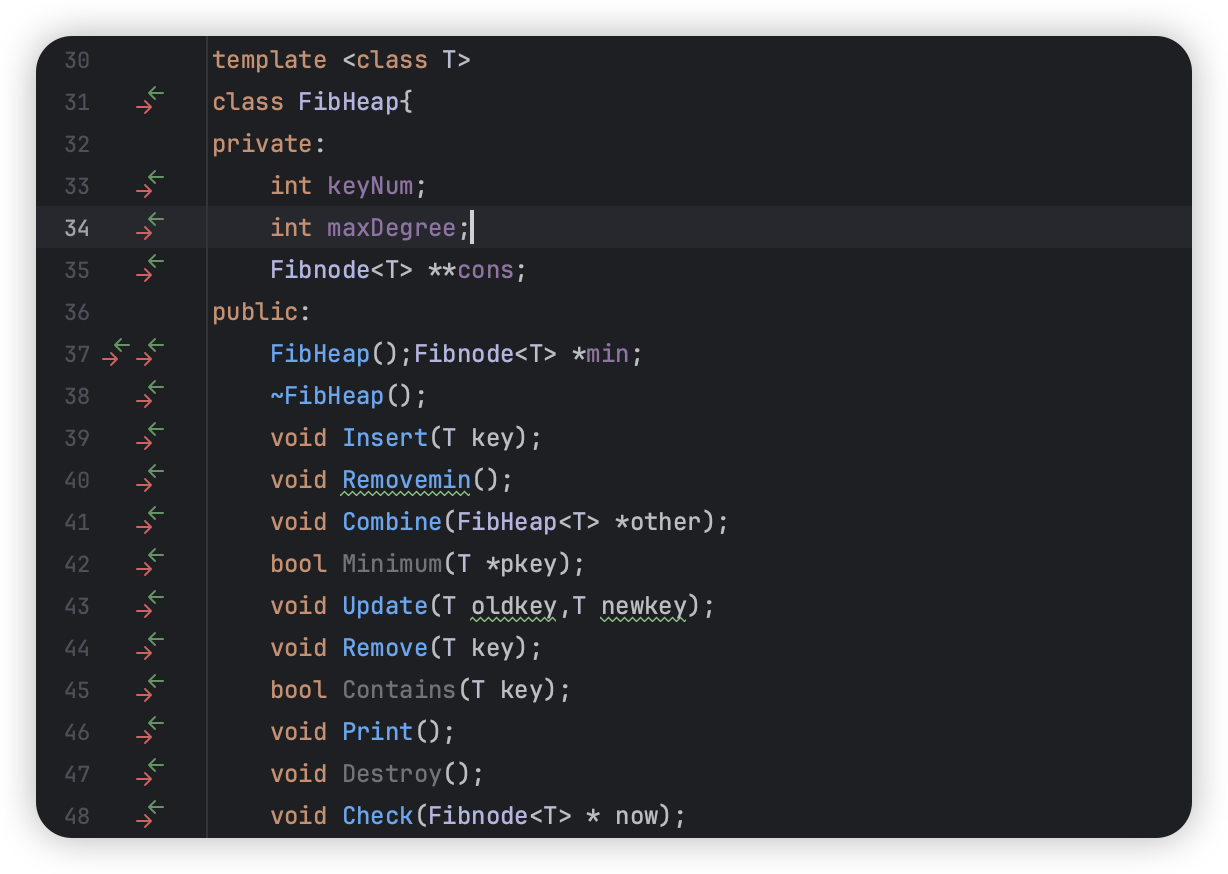
alt text

一步步实现即可。

为了更好的可拓展性，对标stl里的priority_queue，我采用template类模板的方式实现了Fibonacci堆。

这样在之后的qt可视化实验以及dijkstra算法的实验中，可以方便的用不同type的实例化调用Fibonacci堆。

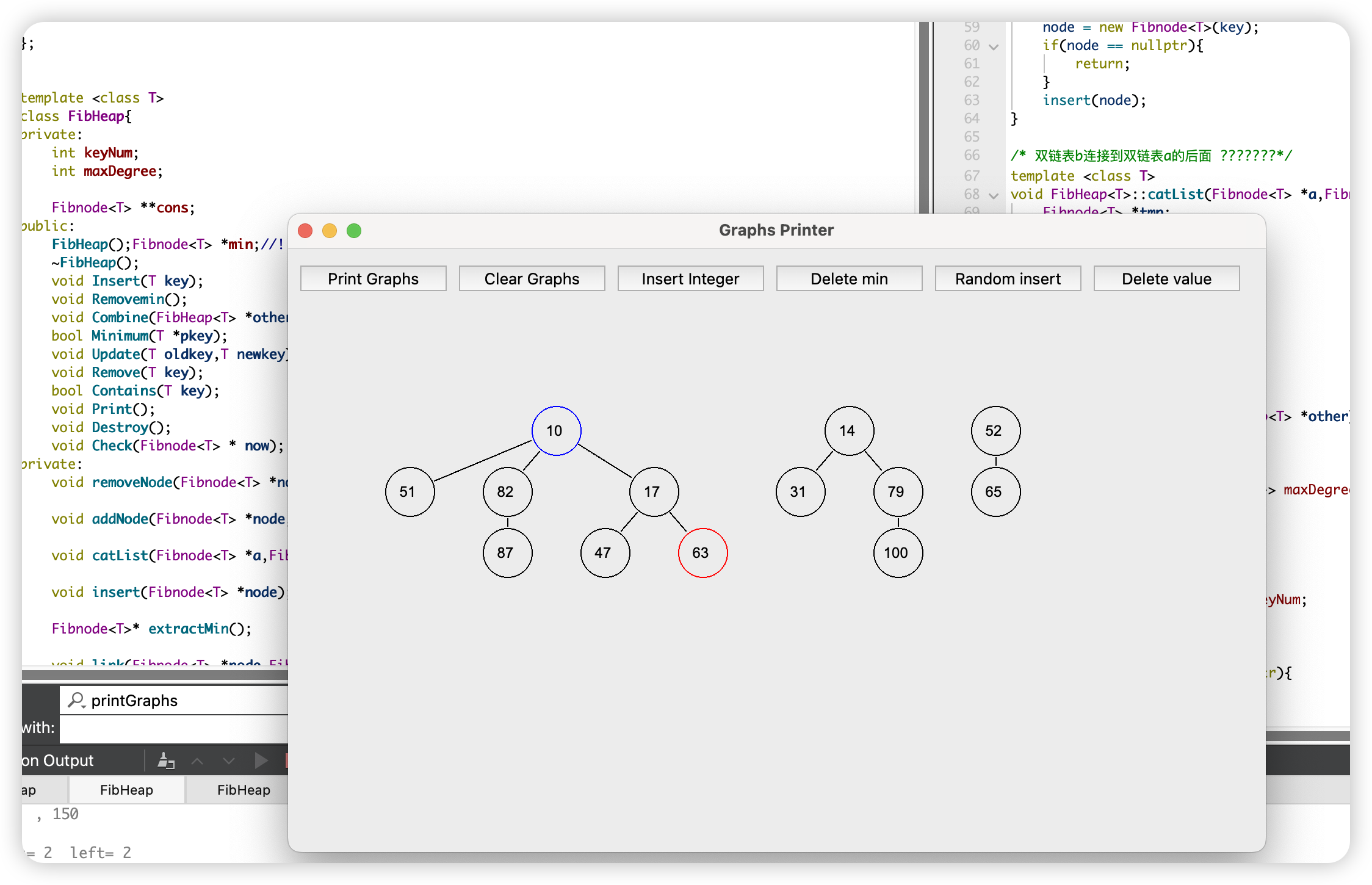
alt text

alt text

alt text

检查了堆性质以及双向链表的正确性。

将上述两点结合起来，在实现从数据结构转化到graph的transform function里，我们可以方便的调试Fibonacci堆。

alt text

这里我使用大量的随机数据以及强力数据（针对一些极限情况的考虑，比如针对spfa最短路算法的最劣图构造）针对dijkstra算法需要的insert和remove_min操作进行了对拍，确保Fibonacci堆的正确性。

这里我主要对比用priority_queue、Fibonacci堆以及list实现的dijkstra算法在随机图和强力图上的表现。

约定，节点数为n，边数为m。

list
insert: $O(1)$
remove_min: $O(n)$
max: $O(n^2)$
priority_queue
insert: $O(\log n)$
remove_min: $O(\log n)$
max: $O((n+m) \log n)$
Fibonacci堆
insert: $O(1)$
remove_min: $O(\log n)$
max: $O(m + n \log n)$

有了可靠的fibonacci堆，我们得以开展有效的对比实验。

为保证对比实验严谨，我使用完全相同的实现方式（包括io接口），只是在堆的选择上进行了更换。

alt text

从上到下，分别是priority_queue和fibonacci堆在同样的十个数据集上运行的时间总和。

可以看到即使打开了对stl特友好的o2优化，fibonacci堆在较弱数据下也有着优势。list的表现是严重超时。

节点在1e5数量级，边在2e5数量级，构图采取了一些极限情况的考虑，比如针对spfa最短路算法的最劣图构造。

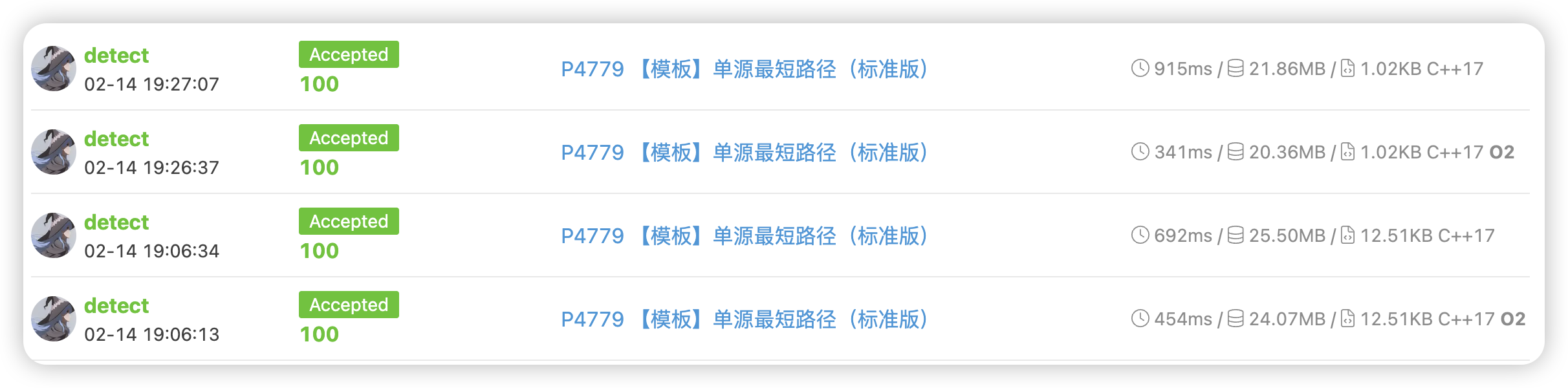
alt text

可以看到，在正常编译环境下，fibonacci堆在强数据下有着更为显著的优势(25% off)。

但是打开o2变异优化后，stl中的priority_queue算法完成了反超，o2对stl系列操作优化太大，另外我手撸的fibonacci堆实现比较粗糙，没有进行过多的优化。

我引用相关论文的实验结果：

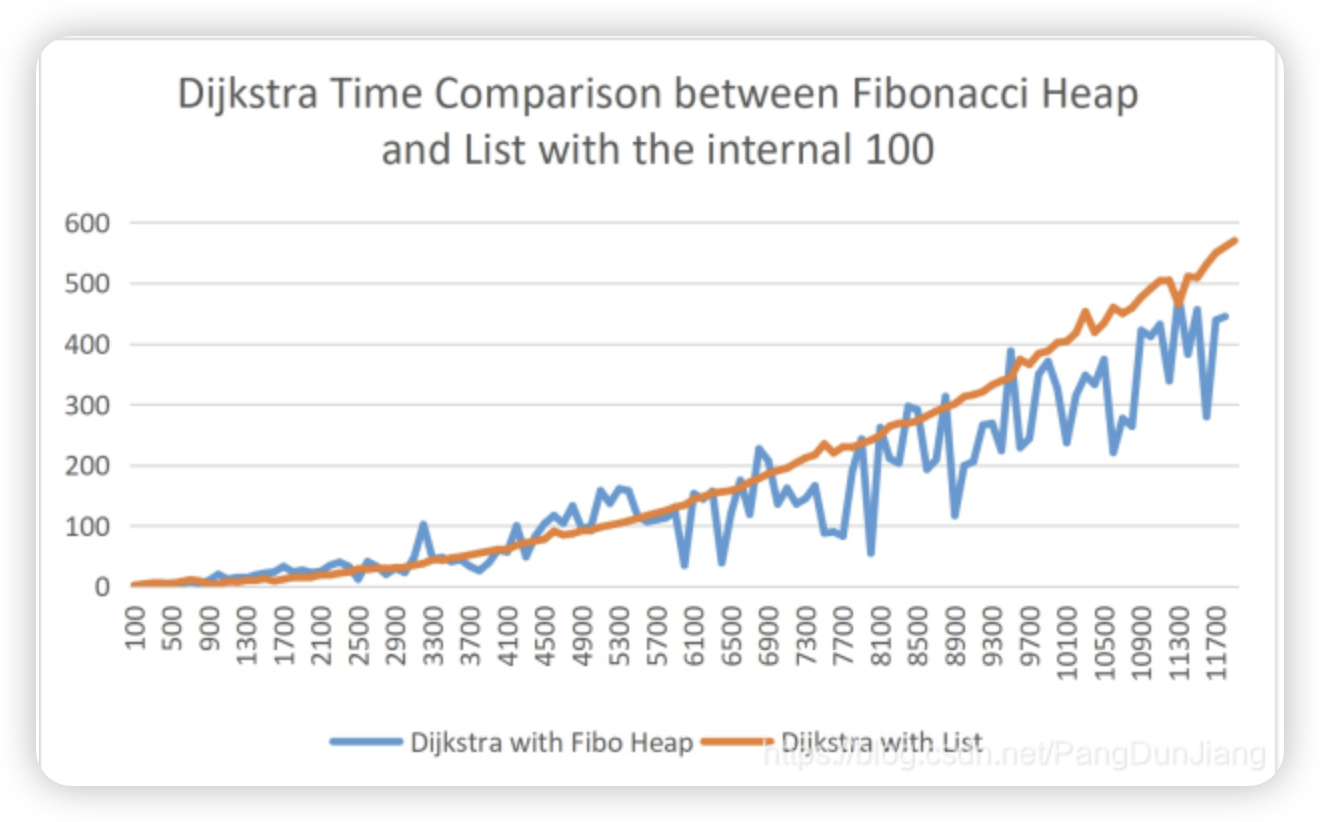
alt text

由于随机图有着许多美好的性质，使得list在随机图上的期望运行时间有很好的上限保证，而fibonacci堆常数较大，此消彼长，在随机图上并没有拉开太大的差距。

最后，对实验结果进行了分析，得出结论：