Crypto note

detect0530@gmail.com

DH key-excahnge protocol

一些公钥系统的安全性定义

这里A甚至可以选择把m0,m1都用pk加密一遍，因为它是CPA，所以这样做是可行。（侧面说明确定性的加密方法在这里不适用）

CCA security

EI Gamal Encryption

注意我们在Gen过程中，随机选择了x，这样就可以保证每次加密的结果都不一样，这样就可以避免确定性加密的问题。

---

但是很遗憾，其不是CCA安全的(个人感觉Dec函数过于简单不是件好事)

RSA

Plain RSA

plain RSA是有问题的

1. 是确定性算法

2. 规约假设中密文是均匀取样才能保证安全性，但是在palin rsa中m不是

Padding RSA

一种实现方法：

打乱了m的分布，同时引入随机性！

例题

数字签名，只要能伪造即可。

一般就是先问几个，然后拼接/运算。

---

solution

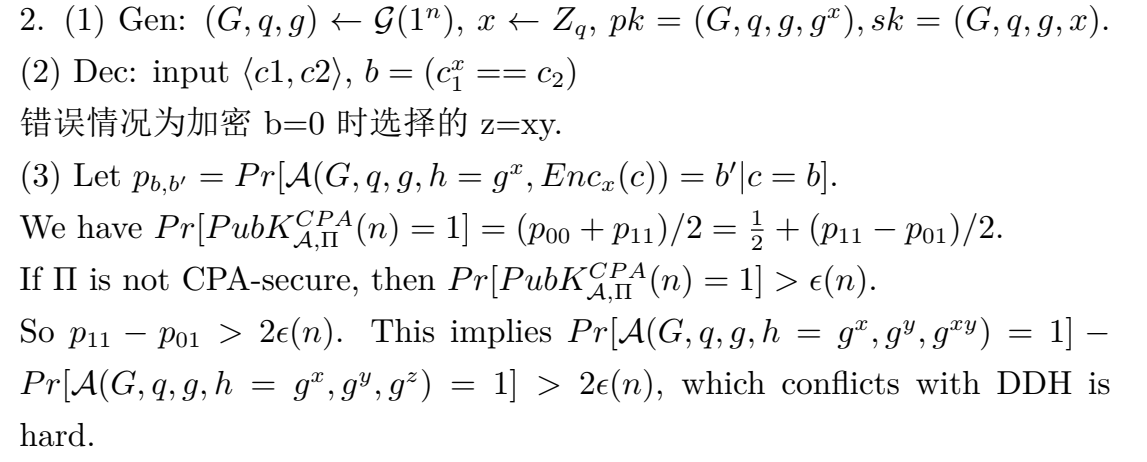
发现这个题希望我们规约到DDH问题。

于是我们分析原问题哪里喝DDH问题相似。

原问题引入b=0/1,分别代表了$(g^x,g^y,g^{xy}) \ (g^x,g^y,g^z)$两种模式。

由ddh假设我们知道，这两种模式的差是不可区分的。

于是就可以像sol那样把赢下来的概率：

$(p_{00}+p_{11})/2 \\ =\frac{1}{2}-(p_{11}-p_{10})$

（把问题转变成了区分离散对数问题）

---

把问题规约到Hash函数不可逆上。

---

一个关键点，存在可以快速判断是个元素使不是二次剩余系。

P=2q+1

如果a是二次剩余，那么$a^q \equiv 1 \ mod \ P$

如果a不是二次剩余，那么$a^q \equiv -1 \ mod \ P$

---

题目的约束其实是，密文长度收到很严苛的限制。

我们可以利用这一点，公钥加密之所以是cpa安全，就是对相同的明文加密，密文是不一样的。

但是由于题目限制了密文长度，也就限制了这种随机性。

我就去试enc(0)，把这个值记下来，就用这个值去detect答案。

因为随机性被长度限制了，随机不能再带来negligible的影响。（被常数c限制了）

---

一些二次剩余系的性质

---

这个问题的关键在于依托于快速二次剩余探测算法，我们可以知晓哪些是二次剩余，哪些不是。

又由于g,h一定是二次剩余，所以如果当m=0时，$c_2$一定是二次剩余。反之，若m随机，则$c_2$以1/2的概率是二次剩余。

用这个可以完成攻击。

---

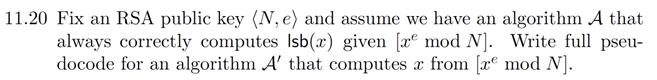
题目给了我们一个lsb的神谕机，可以告诉我们某个数的最低位是0还是1。

于是我们可以问一次，然后通过某种手段把x的最后一位去掉，然后递归地解决这个问题。

可以像sol这样，通过introduce $r=2^{-1}(\mod N)$，然后$x^e \dot r^e = (x\dot r)^e$，完成x的转换，继续调用神谕机。

---

对于签名的安全问题。

用反证法，

如果经过修改，我们的签名不安全了，那么就做一个逆操作，由改造后的签名，引入随机操作，去还原序列，如果改动不大，也就是逆操作成功的概率时多项式的，那么就规约到了已知安全问题，矛盾。