矩阵计算 | detect

矩阵特征值

矩阵的迹

矩阵的秩

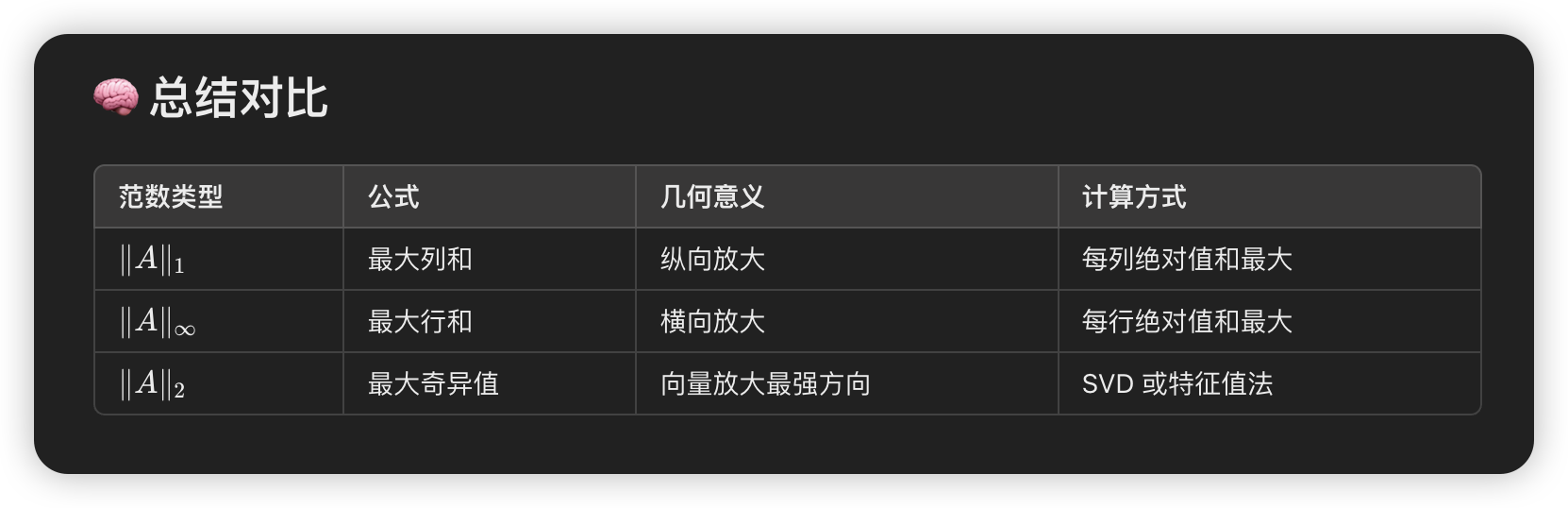
内积and范数

一个比较重要的点：

说明范数之间是有limit的，有时一个范数很难，我们可以转换为最小化另一个容易处理的范数来solve。

正定矩阵

正交矩阵

正交矩阵重要性质：

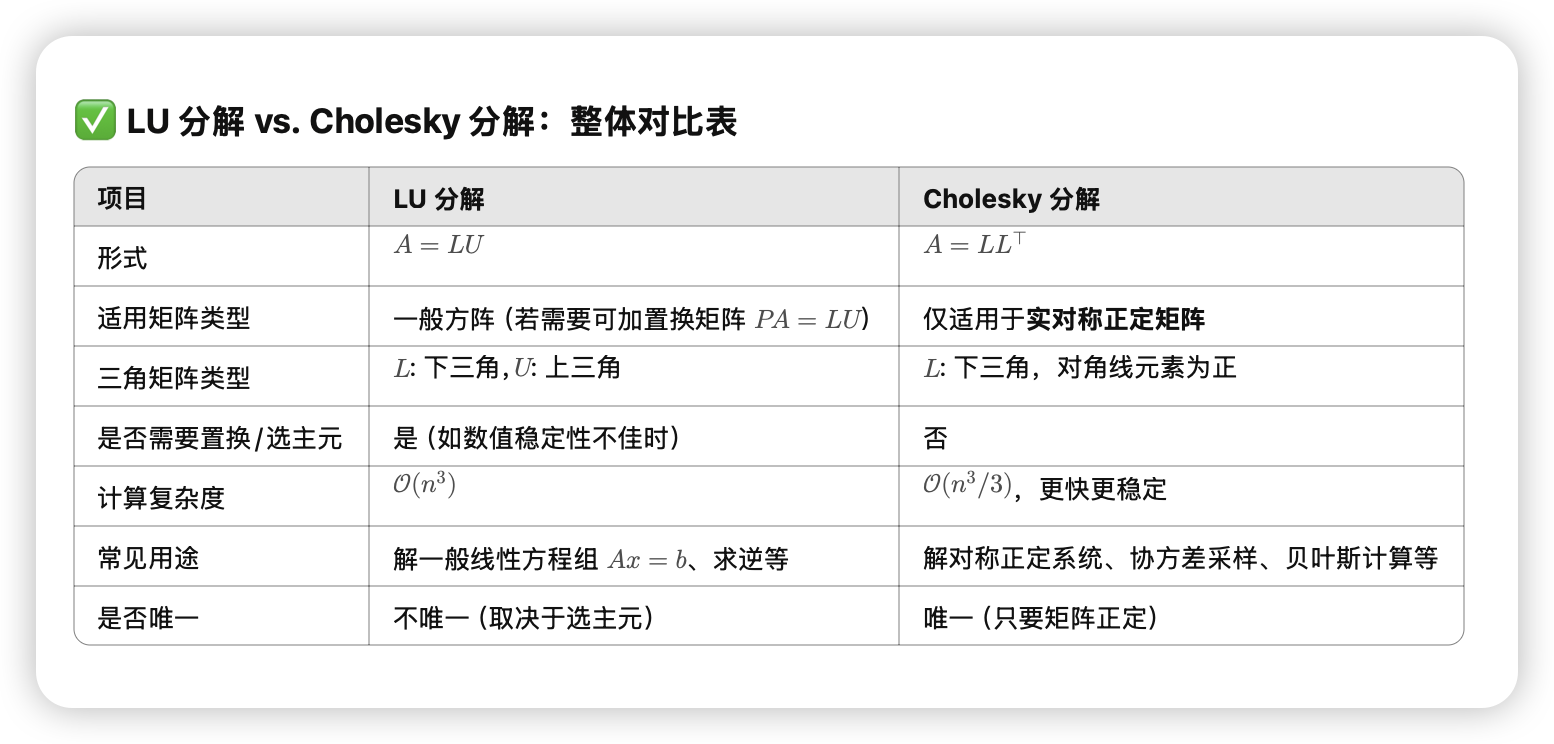
三角矩阵

对于正定矩阵可以有cholesky分解：

这个方法可以用于采样协方差矩阵：

范德蒙矩阵

傅里叶矩阵

特征值分解

所有像 $e^x,sin(x)$ 可以展开成多项式逼近的函数作用在矩阵上都可以先特征值分解做简化。

特征值的定义

对于对称矩阵：

三个对称矩阵特征值特征向量重要的结论：

非对称矩阵在这三个结论上的说法：

挺实用的几个tips。

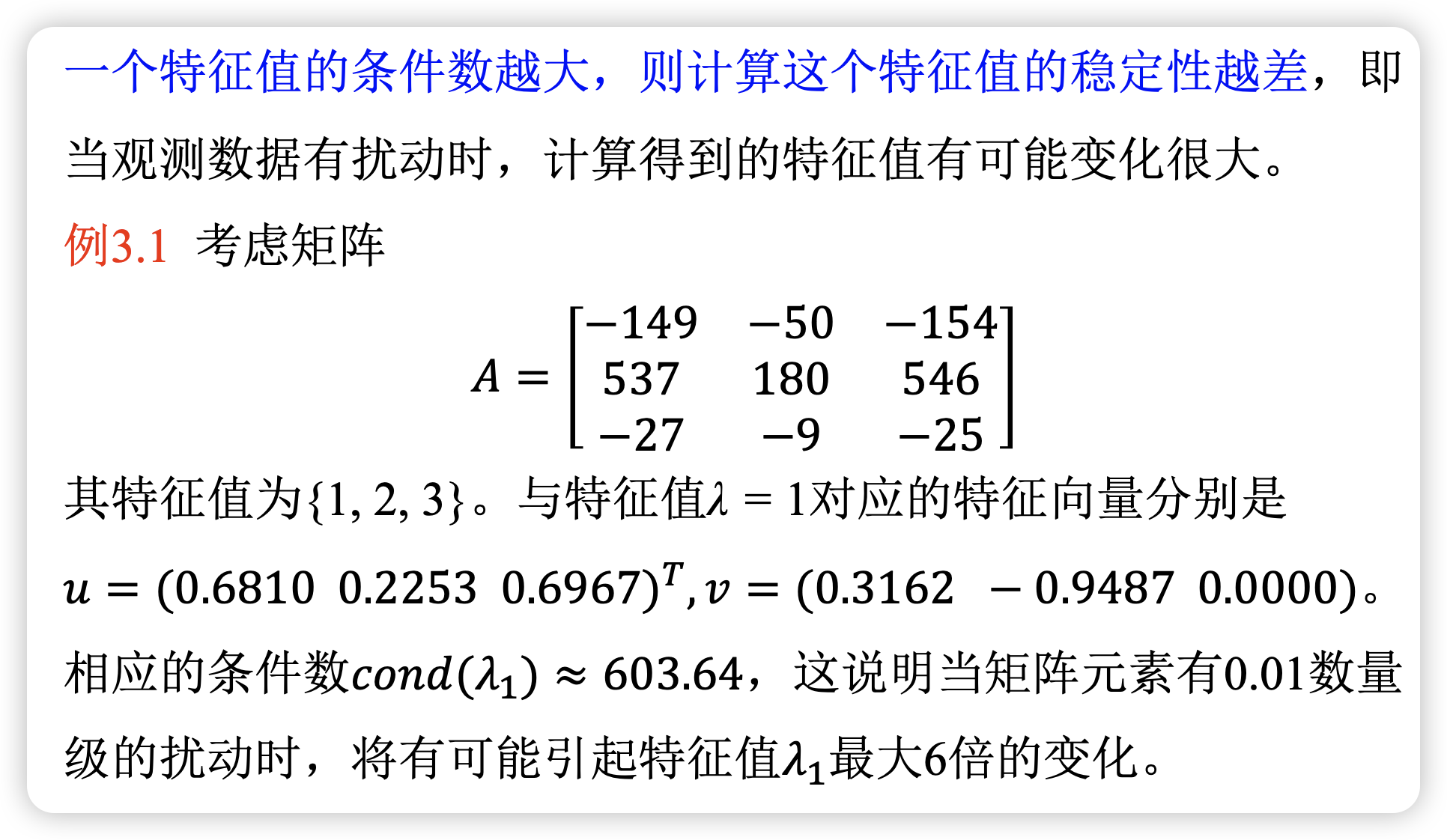
同时这里提到了特征值的条件数

特征值的代数重数大于几何重数

相似矩阵具有相同的特征值：

实对称矩阵一定可以对角化！

对于有重根则需要进一步去算，不一定可以，也不一定不可以。

数值稳定

用二范数的时候，cond就是最大奇异值和最小奇异值的比值。
所以添加对角线eps可以起到稳定作用。

条件数一些性质和应用

QR 分解也是从 $A$ 出发的，为啥我们只说它的条件数是 $\kappa(A)$ ，不是多次出现就变得更坏？

我们来从线性代数和数值分析的角度严谨地解释这个现象。

为什么 QR 分解中不会放大条件数？

📌 一、QR 分解过程是「稳定变换」

QR 分解是：

A = Q R

其中：

$Q$ ：正交矩阵，满足 $Q^H Q = I$ ，不会放大误差（旋转 + 反射操作）
$R$ ：上三角矩阵，决定了解法的“病态程度”

我们把 QR 分解用来解最小二乘问题时：

Ax = b \Rightarrow QRx = b \Rightarrow Rx = Q^H b

现在你注意：

$Q^H$ ：正交矩阵的共轭转置，不会放大向量（ $\|Q^H b\| = \|b\|$ ）
真正解的过程是：解 $Rx = Q^H b$

所以误差传播（condition）主要看的是：

Rx = … 这个系统里， $R$ 的条件数。

而这个 $R$ 的条件数与 $A$ 是一样的（不会平方变差）：

\text{cond}(A) = \text{cond}(R)

所以：

QR 分解虽然用了 $A$ ，但它没有像 $A^H A$ 那样把病态放大。

📌 二、 $A^H A$ 为什么会平方放大？

再复述一下对比：

QR 解法只做了一次操作：从 $A$ 得到 $R$
正规方程法做了：先转置再乘自己 $A^H A$ ，再求逆 —— 相当于对病态矩阵「用力过猛」，错误被放大了两次（平方）

✅ 对比总结表格：

方法	解的形式	条件数级别	放大误差来源
正规方程法	$x = (A^H A)^{-1} A^H b$	$\kappa(A)^2$	来自 $A^H A$ 的平方放大
QR 分解法	$Rx = Q^H b$	$\kappa(A)$	只与 $R$ 有关，等价于 $A$

🔁 回答你最初的问题：

QR 解法中只有一个 A，为什么？

因为：

QR 只是把 A 拆成 $Q$ 和 $R$ ，没有构造 $A^H A$ 这样的“高阶组合”
$Q$ 是稳定的，几乎没有数值影响（单位条件数）
所以唯一影响解的精度的是 $R$ ，而 $R$ 的条件数和 $A$ 相同

奇异值分解

定义：

第三点很重要，提供一个新的视角。

针对第四点：

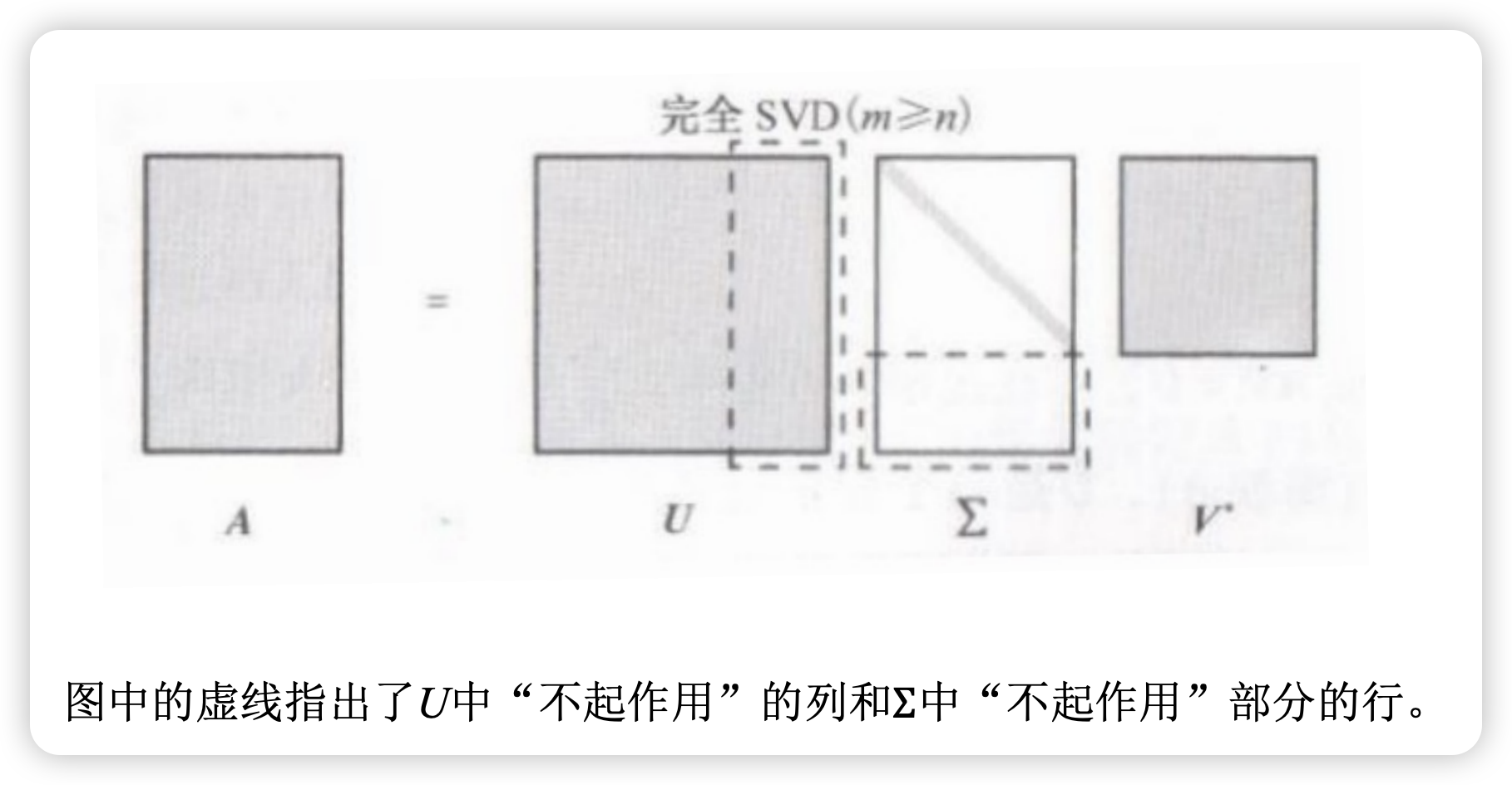
既然奇异值是 0，那后面的列不就“没用”了吗？U 的后 $m - r$ 列不是随便选的吗？它们凭什么说是 $A^H$ 的零空间的正交基？

我们来一点一点拆开这个问题，最后你会发现：这些“看起来没用的列”，恰恰是矩阵结构和零空间分析的关键。

🌟 回顾 SVD 的形式：

对一个 $m \times n$ 的矩阵 $A$ ，做奇异值分解：

A = U \Sigma V^H

$U \in \mathbb{C}^{m \times m}$ ：单位酉矩阵（列是 $A A^H$ 的特征向量）
$V \in \mathbb{C}^{n \times n}$ ：单位酉矩阵（列是 $A^H A$ 的特征向量）
$\Sigma \in \mathbb{R}^{m \times n}$ ：对角线是奇异值 $\sigma_1 \geq \sigma_2 \geq \cdots \geq \sigma_r > 0$ ，其余为 0

假设秩为 $r$ ，则：

\Sigma = \begin{bmatrix} \Sigma_r & 0 \\ 0 & 0 \end{bmatrix}, \quad \text{其中 } \Sigma_r = \text{diag}(\sigma_1, \dots, \sigma_r)

🔍 你的问题聚焦在哪？

你说：

对角线上奇异值后面都是 0，所以乘上去就没用了，那 $U$ 的后 $m - r$ 列不就“没起作用”吗？它们能随便选吗？为什么还能说成是 $A^H$ 的零空间正交基？

✅ 正解：这些“没用”的列恰恰是零空间方向

我们来揭开谜底：

1. 奇异值为 0 ⟹ 对应方向被映射到 0

我们可以看这个结构：

A = \sum_{i=1}^r \sigma_i u_i v_i^H

也就是说：

对于 $v_1, \dots, v_r$ ：会被 $A$ 映射成非零向量
对于 $v_{r+1}, \dots, v_n$ ：对应奇异值为 0，意味着
$A v_i = 0 \Rightarrow v_i \in \text{null}(A)$

所以 $V$ 的后 $n - r$ 列就构成了 $\text{null}(A)$ 的标准正交基

📌 这组列虽然“看起来没用”，但在线性代数意义上是结构的一部分：

SVD 里 $U, V$ 是完整的正交基（单位矩阵）
奇异值为 0 ⟹ 对应方向落入零空间
即使没有贡献在乘法 $A = U \Sigma V^H$ 里，它们仍然有明确的几何/空间意义！

✅ 结论总结

矩阵部分	几何含义	是否“被用到”
$U_{1:r}$	$\text{range}(A)$ 的正交基	✅ 被乘以奇异值
$U_{r+1:m}$	$\text{null}(A^H)$ 的正交基	⚠️ 没有被乘以非零奇异值，但有结构意义
$V_{1:r}$	$\text{row}(A)$ 的正交基	✅ 被乘以奇异值
$V_{r+1:n}$	$\text{null}(A)$ 的正交基	⚠️ 映射为 0，但表征了零空间